Research Interests

I have a number of areas of research that I am currently interested in; all of which I have done work on, am currently working or plan to work on in the future. This page is dedicated to these topics, and I will try my best to keep them updated with my current progress as needed.

Nonlocal Modeling

Nonlocal modeling is a really interesting subject that I started learning about after completing my Masters Thesis work in the Fall of 2013. The idea of nonlocal methods is at-odds with traditional local based approaches like the typical finite element or finite difference type methods. Local based approaches rely on some sort of discretization scheme where the solution at a single node/element/particle(lets call them particles) is determined directly from the solutions of the adjacent particles. Certainly there are ways that you can get around this to increase the extent of how particles interact: higher order basis functions or more complex difference stencils, for example. But at the core local methods are limited by their reach.

The fundamental concept of nonlocal models rests in the fact that they are not constrained to interact with just adjacent particles. Instead, one defines a radius or horizon value that determines how far a given particle can "see" or interact with other particles. This makes solving certain types of problems much more feasible. For example, solutions with discontinuities in them (like cracks, shocks etc.) are difficult to approximate with traditional local methods due to the spatial derivatives inherent in them. With nonlocal methods, there are no spatial derivatives so solutions with discontinuities are much easier to solve!

One unfortunate consequence of these nonlocal methods is the computational cost that comes with them. :( Because of the horizon, generally the linear system bandwidth is much larger than traditional local based approaches. Thus the cost of solving these types of problems is much higher. But with the increase computational power that is being realized even as you read this, cost is becoming slightly less of an issue. Additionally, I am interested in looking at other methods that can be used to speed up the process a little bit, such methods like reduced order modeling(see next section).

Currently (Fall 2015) I am working with my advisors to get a paper out about coupling reduced order approaches to nonlocal problems when that is submitted/approved etc. I will post it here.

Reduced Order Modeling

Reduced Order Modeling (ROM) is computational technique that is used to reduced the number of degrees of freedom in a system using intelligent information. Applications for this include situations where a large simulation must be executed in a short amount of time with a good amount of precision. When I say "large simulation," I mean something that could take hours or potentially days to run. But in cases where time is a priority, running large simulations might not be possible.

A prime example of a situation described above, would be an outbreak of some new deadly strain of virus. When something like this happens, we may not have days, or even hours, to predict how this virus will spread. But with ROM, we have the ability to run this simulation at a fraction of the amount of time with decent precision.

Here are some resources that I have worked on that use Reduced Order Modeling:

• A short presentation on how ROM is used in a a fluid dynamics simulation for the flow over a sphere at varying Reynolds numbers
• The work I did for my Master's Thesis on applying a Reduced Order Model to the Wavelet-Galerkin Approximation of Differential Equations

Computational Fluid Dynamics and The Finite Element Method

Computational Fluid Dynamics (CFD) has become one of the most widely studied areas of Engineering research over the past couple of decades. With the increase in computational power and the ability to store large amounts of information, larger simulations that previously seemed out of the realm of imagination are now possible. CFD is used in a number of applications from simple water tank:

to flow over a high-lift aircraft wing:

Typically researchers and engineers alike will use the finite element method (FEM) to solve CFD problems. The finite element method is a computational technique that is used to solve differential equations using a sets of basis functions to represent the actual solution with a numerical one. These basis functions are in general only defined over a small subset of the domain that you are trying to represent. The reason that the finite element method has become the go-to method for CFD problems is its adaptability to solving all sorts of problems. For example unstructured meshes like the one shown below, are easily integrated into a FEM simulation.

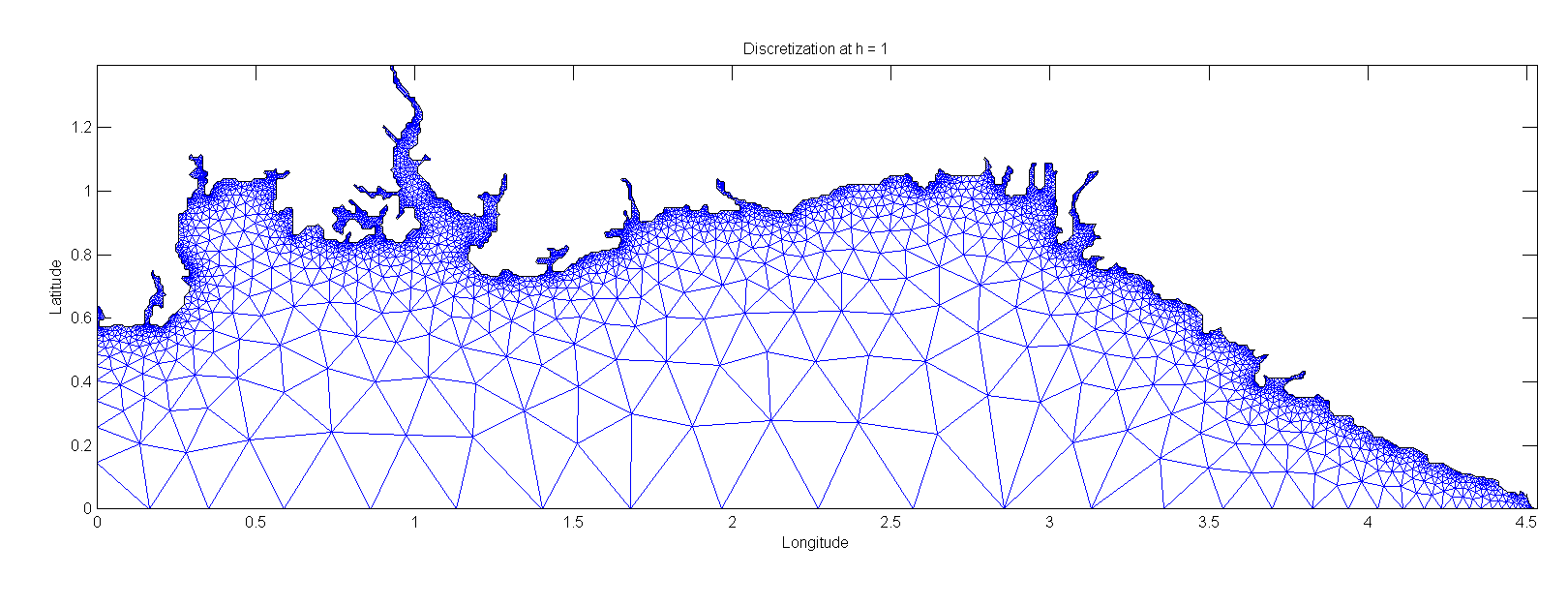
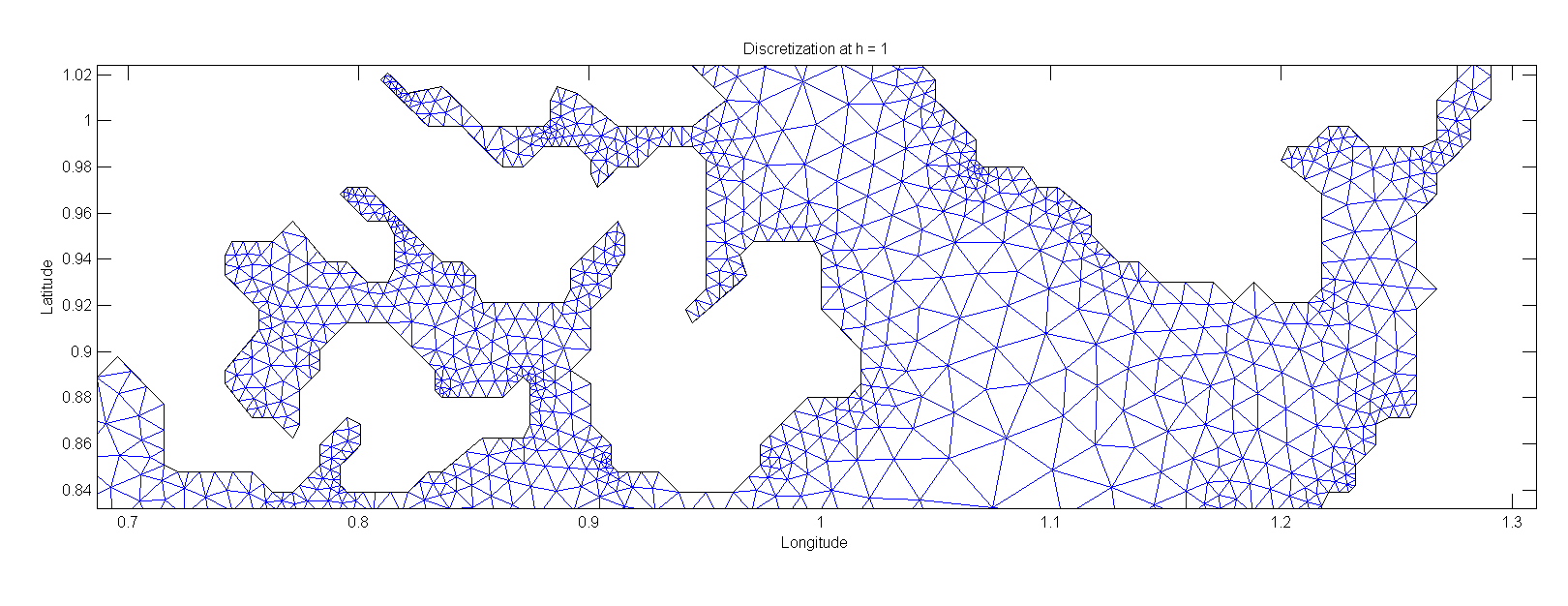
Figures 1-3 were from a FEM project that I worked on to solve a PDE using an unstructured mesh with triangular elements and barycentric coordinates. The report and code can be found here.

Machine Learning Applications

Although it seems like computers and technology are taking over the world, they can't think for themselves, so there is no way they could overthrow the human population and rule over us Terminator style right? Maybe... Over the past decade and a half or so, we have gotten increasingly better at creating machines and software that "thinks" for itself. Mostly the thought process is the same as ours; use data that we have previously encountered to make real-time decisions. In fact this webpage is most likely periodically crawled by Google's and others software to determine the type of information contained in it, so that a search algorithm can present customized search results to users that it believes would have the most interest in such a website. Perhaps that is why you are reading this...

Machine Learning is everywhere nowadays and will continue spreading as more and more people find new ways that it can be applied. One such application that I worked on was using machine learning, and specifically Support Vector Machines (SVM) to predict gas-turbine airfoil geometry. This project uses sample data that is in no way realistic of any airfoil that has or will be made, any similarities are purely accidental.

The problem we were trying to solve was: how to predict whether a set of geometric inputs would result in a viable airfoil. When I say viable airfoil I mean that the interior cooling mechanism is fully contained and the other geometric sizes would fit the constrained space it must be confined in. Previously, the process would involve running some bothersome software that would construct the airfoil based on some geometric properties and then tell us whether it was viable or not. Unfortunately this took time and wasn't very good if you wanted to run some sort of optimization and only wanted to test airfoils that worked. You had no way of knowing whether the airfoil would be viable or not so we wanted to try out some way to predict what types of airfoils would succeed given a set of geometric inputs, so that optimizations could focus on those areas.

Again any of the data that is contained within this project is fictional and has no relation to any airfoil ever or to be produced. The code and literature from this project can be found here.