1. Crystallization of Copolymers from Solutions

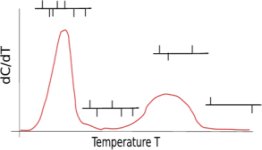Copolymerization is used to tune the properties of man-made plastics, for example to regulate crystallinity, to enhance mechanical properties, and to expand the temperature performance window by incorporating one or more comonomers into a homopolymer chain. These properties are governed by the details of the chain microstructure, i.e. distribution of comonomers and the molecular weight. These distributions are crucial to establish structure-property relationships, and to monitor product quality. The analytical techniques commonly used to characterize the chemical composition distribution (CCD) of semicrystalline binary ethylene/olefin copolymers, such as Crystaf and solution DSC, are based on the relationship between the thermodynamic driving force for crystallization and the branching content. In these copolymers the longer the ethylene sequences between branches, the more stable the polymer is in solution. The length of the segment between branches decreases as comonomer content increases. Consequently, copolymer chains with more short chain branches crystallize at lower temperatures, forming thinner lamellae and less perfect crystallites.

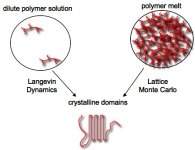Thus, our strategy is two-pronged. At an engineering level we seek to build mechanistic models to predict Crystaf curves from the chemical composition, and vice versa. There are a number of unsolved problems in the theory of nonisothermal crystallization of copolymers from solutions. At the fundamental level we seek to get a glimpse into these processes using Langevin dynamics and kinetic Monte Carlo models.

2. Cyclic Polymers

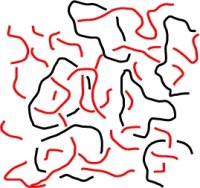Concentrated solutions of ring or cyclic polymers (CPs), which lack chain ends, are scientifically intriguing, since they defy a simple description in terms of the tube model which has been used rather successfully to describe the properties of linear and branched polymers. My focus is the on the statics and dynamics of blends of cyclic and linear polymers. These blend systems are important for two reasons: (i) most experimental data on pure CPs are, in fact, data on cyclic-linear blends (CLB), due to contamination or limitations of purification methods, and (ii) the dynamics of such CLBs, are extraordinarily sensitive to the concentration of linear polymers, as demonstrated by the linear viscoelastic and self-diffusion studies. These studies indicate a dramatic change in the mobilty of CPs that is, both, unexpected and unexplained, and might supply deep insights into entangled polymer dynamics. Recent simulations seem to indicate that CLBs might be ideal systems to unravel the controversial process of constraint release.

A recent presentation on some of this material at ICR 2008 (pdf)

3. Microscopic Simulations of Concentrated Polymer Solutions and Melts

The wide separation of dynamical timescales, ranging from the order of pico-seconds for inter-atomic oscillations, to the order of hours for phenomena of greatest relevance to polymer processing, makes it practically impossible to describe the complete dynamics of concentrated polymer solutions and melts using a single modeling methodology (like molecular dynamics, for example). 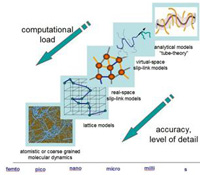Therefore, a number of coarse-grained microscopic and mesoscopic models have been developed in which all the action occurring at fast local levels is smeared out, and attention is focused only on slower modes of motion which control properties such as viscosity.

In order to encompass the broad spectrum of timescales (about 10 decades), we are interested in developing an "overlapping" multiscale modeling strategy such as that outlined in the figure above. "Detailed" models include simulation methods such molecular dynamics and the bond-fluctuation lattice models which are coarse-grained at the Kuhn-step level (~1 nm). In general, these detailed simulations can be used to question, justify, or reject certain assumptions made in coarse-grained models, and progressively improve these coarse-grained models. We are particularly interested in how sub-chain level mechanisms can be interpreted and recast into the parameters describing the mean-field "tube model". We expect the cross-talk between various levels of modeling to open up, and shape future directions of inquiry.

A presentation on some of this material at SoR 2007 (pdf)

4. Rheology of Branched Polymer Melts

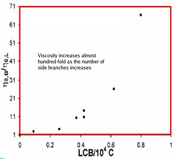The rheological responses of linear chains, and "comb"-like molecules, with long side chains along a linear backbone, are dramatically different. For example, a minute degree of long-chain branching (LCB), of the order of one side branch per 10,000 backbone carbon atoms, can jack up the zero-shear viscosity of a linear chain by a factor of 100. At the same time, LCB endows the polymer melt with desirable processing properties such as shear thinning (thus low energy during process such as molding and extrusion) and strain hardening (thus, they resist tear during film blowing operations). Thanks to advances in metallocene-based catalyst technology, LCB in polyolefins can be administered and controlled to an unprecedented degree.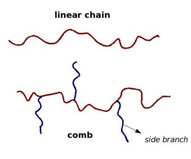

The threshold of conventional methods of chemical analysis like spectroscopy and chromato-graphy in detecting sparse structural details, like low concentrations of LCB, is far below a level that can be considered adequate from an industrial perspective. The sensitivity of rheology to molecular architecture and branching details has spawned the notion of analytical rheology - the idea that linear viscoelastic measurements can be used to probe the underlying molecular structure of polymers. Work in this area attempts to build, primarily, upon the standard tube theory for polymer melts. To complement theoretical work, we also use mesoscopic simulation models, such as the slip link model which is coarse-grained at the level of the "tube" diameter (a few nanometers in melts). Linear viscoelastic data on a wide variety of linear and branched polymer may be downloaded in the form of a tar-zipped file tar-zipped file.

A presentation on some of this material at ACS 2006 (pdf)

5. Modeling for Tissue Engineering Applications

Coaxing cells to produce functional tissue requires their cultivation and organization on 3D substrates, or scaffolds. These scaffolds act as a surrogate for the extra-cellular matrix found in the human body. A wide range of materials and manufacturing methods for the synthesis of 3D scaffolds have been developed. However, the development of scaffolds is beset with a variety of challenges, including tissue ingrowth that is limited to the exterior of the scaffold due to insuffcient nutrient and product transport, and loss of cellular phenotype due to improper cell-matrix, cell-cell interaction and signaling.

Recently, highly uniform and organized tissue engineering scaffolds possessing inverted-colloidal crystal (ICC) geometry, which are inexpensive to manufacture and do not suffer from material constraints, have been developed. Due to the regularity of these ICC scaffolds, computational modeling functions as an important tool to explore the vast available design space and to develop novel assays. For example, in the past we have use borrowed Langevin dynamics (widely used in the polymer and colloids literature) to characterize the transport of nutrients/metabolic products through the porous ICC scaffolds, and to quantify the extent of cell-matrix interaction and cell-cell interactions. These studies have been used to optimize scaffold geometry for particular cell lines, and have been validated experimentally.

Currently, we are trying to develop models that reflect some the complexity and richness inherent in biological systems. For instance, cells have anisotropic shapes and cell-cell and cell-matrix interactions are usually highly specific. To incorporate these processes, current and future research is aimed on developing mesoscopic cellular automata and agent-based models.

6. Modeling for Nanotechnology Applications

In the past few decades, substantial progress has been made in describing transport and quantum mechanical phenomena in nanocrystals (NCs). As a next step, one must consider the organization or integration of these NCs into optical or electronic devices. This inevitably requires us to understand the nature and magnitude of inter-particle interactions, since these very forces govern and dictate their "self-assembly" properties, interactions with other nanoscale entities, and methods of manufacturing. Dipole moment is one such fundamental force, and in the past, we have examined the origin of large anomalous dipole moment (~50-100 debye) in centero-symmetric cubic nanocrystals. The energy associated with this polarity can overcome random thermal fluctuations, and regulate interactions with other nanoscale species such as proteins, as well as influence the thermodynamics of charge-transfer processes.

We have also examined the kinetics of unusual higher order structures such as checkmarks starting from Tellurium nanorods, using Brownian dynamics simulations. In general, such simulations, when used as a tool-kit in conjunction with synthesis, can be used to explore the available design space to suggest and exploit synthetic routes that might not be immediately obvious.