spiral_pde_movie, a MATLAB code which solves a pair of reaction-diffusion partial differential equations (PDE) over a rectangular domain with periodic boundary condition, whose solution is known to evolve into a pair of spirals. The sequence of solutions is bundled into a movie.
The equations to be solved approximately involve the Laplacian operator. The user has a choice of several functions that can estimate this value. The version using a 5 point stencil produces spiral solutions that are somewhat square in shape, while the 9 point stencil produces a rounder and more symmetric spiral.
The PDE has the form:
du/dt = del u + u * ( 1 - u ) * ( u - ( v + beta ) / alpha ) ) / epsilon
dv/dt = delta * del v + u - v
The domain is the square 0 <= x <= 80, 0 <= y <= 80, with zero Neumann boundary conditions.
The initial conditions are
u = 0 for x < 40
1 for 40 < x
v = 0 for y < 40
alpha/2 for 40 < y
The parameters are
alpha = 0.25
beta = 0.001
delta = 0.0
epsilon = 0.002
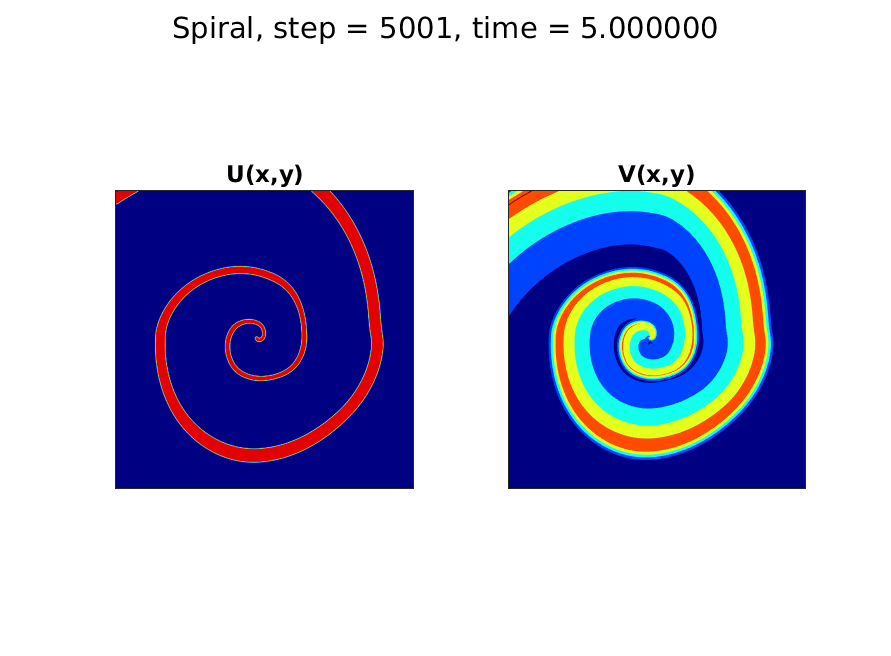
Here is an image of the pair of solutions at time t=5:

The information on this web page is distributed under the MIT license.
spiral_pde_movie is available in a MATLAB version.
cavity_flow_movie, a MATLAB code which animates the velocity solutions for the driven cavity;
cvt_1_movie, a MATLAB code which creates an animation of the evolution of a Centroidal Voronoi Tessellation (CVT) in the unit square.
cvt_2_movie, a MATLAB code which animates the generation of a Centroidal Voronoi Tessellation (CVT) in the unit square, which includes a random "rebirth" at every iteration.
cvt_3_movie, a MATLAB code which animates the generation of a Centroidal Voronoi Tessellation (CVT) for the "holey pie" region.
cvt_4_movie, a MATLAB code which creates a Centroidal Voronoi Tessellation (CVT) movie in a square, with a density function that drives points to the corners;
cvt_corn_movie, a MATLAB code which makes a movie in which the growth of a corn kernel is simulated using a Centroidal Voronoi Tessellation (CVT).
gray_scott_movie, a MATLAB code which solves versions of the partial differential equation (PDE) known as the Gray-Scott reaction diffusion equation, converting the solutions to a sequence of graphics frames, which are then assembled into a movie.
peak_movie, a MATLAB code which creates a sequence of frames, and then an animation or movie from the data displayed by the peaks() function.
pendulum_double_ode_movie, a MATLAB code which solves the double pendulum ordinary differential equation (ODE) for a given set of initial conditions and parameters, and makes a movie of the results.
shallow_water_1d_movie, a MATLAB code which solves the partial differential equation (PDE) known as the shallow water equations (SWE), converting the solutions to a sequence of graphics frames, which are then assembled into a movie.
tetrahedron_slice_movie, a MATLAB code which is given a tetrahedron and a vector, displays an evenly spaced sequence of planes that intersect the tetrahedron and are normal to the vector, and creates a movie of the process.