The Lineup Puzzle
Solution

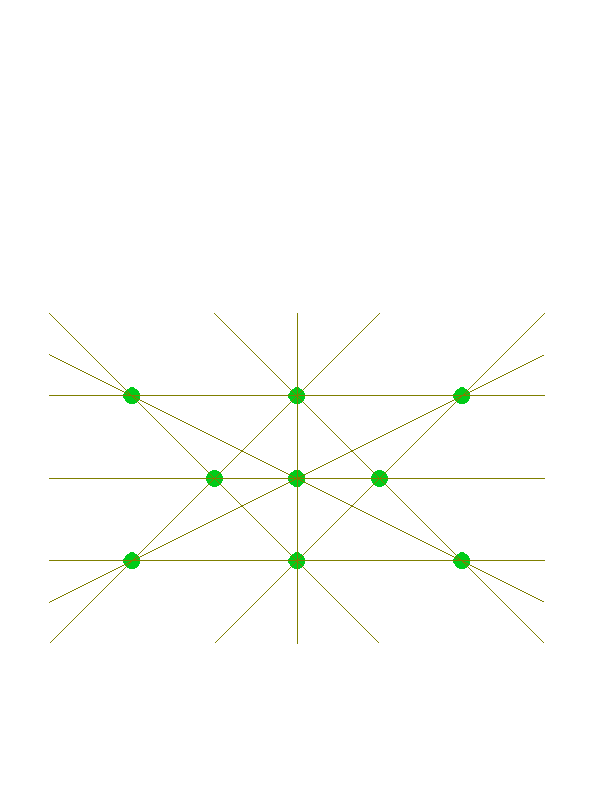
Puzzle 1: If you start with a 3 by 3 square that has 8 lines, you can easily modify it to create 10 lines by sliding the four corner points left and right. Now we have 3 horizontal lines, 1 vertical, and the 2 diagonals; we've lost two vertical lines, but we've gained 4 new lines that join the corner points, an endpoint of the middle row, and the middle of the top or bottom row.

Here is a table based on Gruenbaum, giving the number of trees, and the maximum number of rows of 3 that can be produced. Values which are not known to be the best have a question mark.

Number of trees	Rows of 3
3	1
4	1
5	2
6	4
7	6
8	7
9	10
10	12
11	16
12	19
13	22?
14	26?
15	31?
16	37
17	40?
18	46?
19	52?
20	57?

Puzzle 2: you can arrange 10 pennies into 5 rows of 4 by placing them in a star pattern:

 
              *

        *   *   *   *

           *     *
              *
          *       *
      

Puzzle 3: You can arrange 16 points in such a way that there are 15 lines of 4 points [Dudeney]. To do this, place three nested pentagons around a center point. The first pentagon can be of arbitrary size, but symmetric about the center point. To determine the second one, draw a star inside the first pentagon; this star will circumscribe the second pentagon. Draw a star inside the second pentagon to determine the third pentagon. The 16 points then comprise the vertices of the three pentagons, and the center point.

Here is a table based on Gruenbaum, giving the number of trees, and the maximum number of rows of 4 that can be produced. The values are known to be the best possible through N = 12.

Number of trees	Rows of 4
4	1
5	1
6	1
7	2
8	2
9	3
10	5
11	6
12	7
13	9?
14	10?
15	12?
16	15?
17	15?
18	18?
19	19?
20	21?
21	23?

Here is a table based on Gruenbaum, giving the number of trees, and the maximum number of rows of 5 that can be produced. Most of these results have not been proven to be maximal.

Number of trees	Rows of 5
5	1
6	1
7	1
8	1
9	2
10	2
11	2
12	3
13	3
14	4
15	6
16	6
17	7
18	9
19	10
20	11
35	36

Reference:

1. Pierre Berloquin,
   100 Geometric Games.
2. Henry Dudeney,
   Amusements in Mathematics,
   Originally published in 1917.
3. Martin Gardner,
   Tree-Plant Problems,
   Time Travel and Other Mathematical Bewilderments,
   Freeman, 1988.
4. Branko Gruenbaum,
   New Views on Some Old Questions of Combinatorial Geometry,
   Teorie Combinatorie,
   Volume 1, 1976, pages 451-468.

Back to the The Lineup Puzzle.