 |
 |
 |
Algorithms for image processing
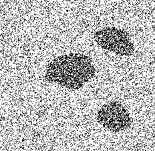
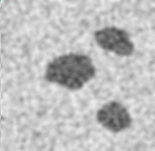
A centroidal Voronoi tessellation (CVT )is a special Voronoi tessellation for which the generators of the Voronoi regions in the tessellation are also the centers of mass (or means) with respect to a prescribed density. In the image processing context and in its simplest form, the CVT-based methodology reduces to the well-known k-means clustering technique. However, by viewing the latter within the CVT context, very useful generalizations can be easily made; several such generalizations are exploited in my research. We have designed CVT-based algorithms for image compression and segmentation applications. These include the basic CVT method and generalizations that include cluster dependent weights, the incorporation of averaging techniques to treat noisy images, extensions to treat multi-channel data for image denoising, and combinations of the aforementioned techniques. In each case, experiments are conducted to illustrate the effectiveness of CVT-based image processing methodologies [1].
Examples:
 |
 |
 |
Detect the mine field from noised picture.
 |
 |
 |
|
Detect 'S' in original picture.
 |
 |
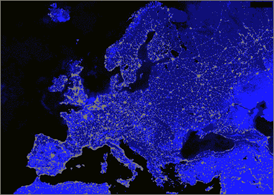 |
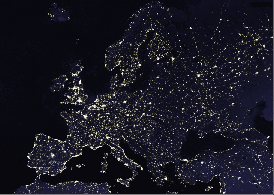
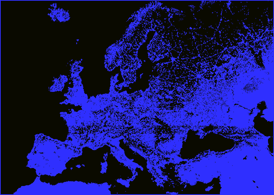
Segmentation of the Europe in night picture: Middle (2
clusters); Right (4 clusters).
 |
 |
 |
 |
Airplane detection from pictures of two channels.
![]()
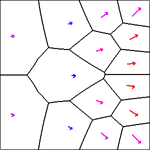
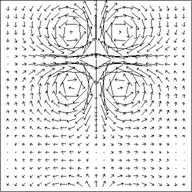
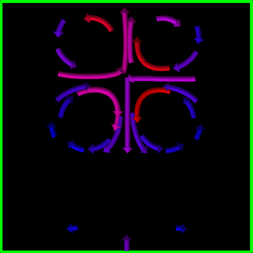
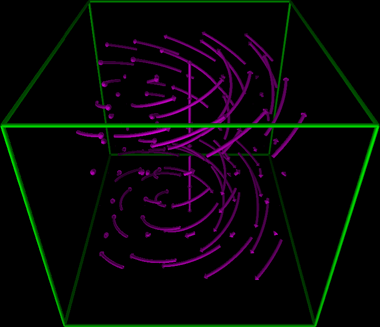
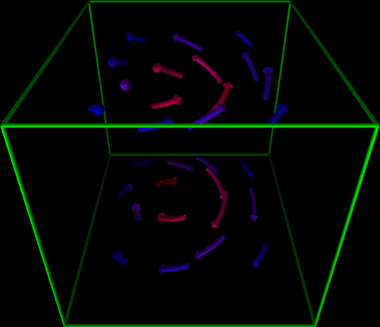
We developed a new algorithm for the simplification and the visualization of vector fields [2]. A one-sided distance function in both the spatial and vector spaces is introduced to measure the similarity of the spatially distributed vector fields. Based on such a distance, vector fields are naturally clustered in the CVT framework and their simplified representations are obtained. Our method combines simple geometric intuitions with the rigorously established optimality properties of the CVT. It is simple to describe, easy to understand and implement. We provided many numerical examples to illustrate the effectiveness and competitiveness of this CVT-based vector simplification and visualization methodology.
Examples:
 |
 |
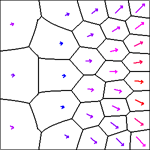 |
15 and 30 clustering of a vector
field
 |
 |
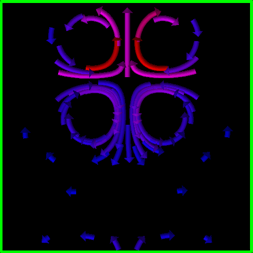 |
2-d Visualization of the vector field by 15 and 30 vectors
 |
 |
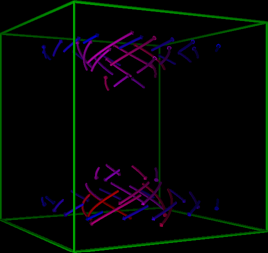 |
3-d Visualization of the vector field by 15 and 30 vectors
|
|
References |
- Centroidal Voronoi tessellation algorithms for image compression and segmentation, with Qiang Du, Max Gunzburger and Lili Ju, accepted to publication in Journal of Mathematical Imaging and Vision, 2005
- Centroidal Voronoi tessellation based algorithms for vector fields visualization and segmentation, with Qiang Du, IEEE Proceedings of Visualization 2004 (VIS2004), (regular paper), Austin, Texas, pp43-50, 2004