% Section 6.2, Boyd & Vandenberghe "Convex Optimization"
% "Just relax: Convex programming methods for subset selection
%  and sparse approximation" by J. A. Tropp
% Written for CVX by Almir Mutapcic - 02/28/06
%
% We consider a set of linear inequalities A*x <= b which are
% feasible. We apply two heuristics to find a sparse point x that
% satisfies these inequalities.
%
% The (standard) l1-norm heuristic for finding a sparse solution is:
%
%   minimize   ||x||_1
%       s.t.   Ax <= b
%
% The log-based heuristic is an iterative method for finding
% a sparse solution, by finding a local optimal point for the problem:
%
%   minimize   sum(log( delta + |x_i| ))
%       s.t.   Ax <= b
%
% where delta is a small threshold value (determines what is close to zero).
% We cannot solve this problem since it is a minimization of a concave
% function and thus it is not a convex problem. However, we can apply
% a heuristic in which we linearize the objective, solve, and re-iterate.
% This becomes a weighted l1-norm heuristic:
%
%   minimize sum( W_i * |x_i| )
%       s.t. Ax <= b
%
% which in each iteration re-adjusts the weights W_i based on the rule:
%
%   W_i = 1/(delta + |x_i|), where delta is a small threshold value
%
% This algorithm is described in papers:
% "An Affine Scaling Methodology for Best Basis Selection"
%  by B. D. Rao and K. Kreutz-Delgado
% "Portfolio optimization with linear and �xed transaction costs"
%  by M. S. Lobo, M. Fazel, and S. Boyd

% fix random number generator so we can repeat the experiment
seed = 0;
randn('state',seed);
rand('state',seed);

% the threshold value below which we consider an element to be zero
delta = 1e-8;

% problem dimensions (m inequalities in n-dimensional space)
m = 100;
n = 50;

% construct a feasible set of inequalities
% (this system is feasible for the x0 point)
A  = randn(m,n);
x0 = randn(n,1);
b  = A*x0 + rand(m,1);

% l1-norm heuristic for finding a sparse solution
fprintf(1, 'Finding a sparse feasible point using l1-norm heuristic ...')
cvx_begin
  variable x_l1(n)
  minimize( norm( x_l1, 1 ) )
  subject to
    A*x_l1 <= b;
cvx_end

% number of nonzero elements in the solution (its cardinality or diversity)
nnz = length(find( abs(x_l1) > delta ));
fprintf(1,['\nFound a feasible x in R^%d that has %d nonzeros ' ...
           'using the l1-norm heuristic.\n'],n,nnz);

% iterative log heuristic
NUM_RUNS = 15;
nnzs = [];
W = ones(n,1); % initial weights

disp([char(10) 'Log-based heuristic:']);
for k = 1:NUM_RUNS
  cvx_begin quiet
    variable x_log(n)
    minimize( sum( W.*abs(x_log) ) )
    subject to
      A*x_log <= b;
  cvx_end

  % display new number of nonzeros in the solution vector
  nnz = length(find( abs(x_log) > delta ));
  nnzs = [nnzs nnz];
  fprintf(1,'   found a solution with %d nonzeros...\n', nnz);

  % adjust the weights and re-iterate
  W = 1./(delta + abs(x_log));
end

% number of nonzero elements in the solution (its cardinality or diversity)
nnz = length(find( abs(x_log) > delta ));
fprintf(1,['\nFound a feasible x in R^%d that has %d nonzeros ' ...
           'using the log heuristic.\n'],n,nnz);

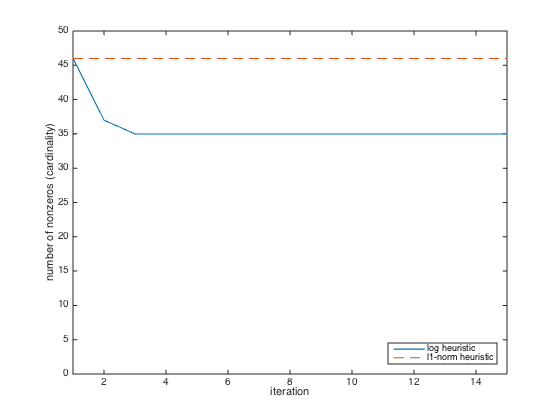
% plot number of nonzeros versus iteration
plot(1:NUM_RUNS, nnzs, [1 NUM_RUNS],[nnzs(1) nnzs(1)],'--');
axis([1 NUM_RUNS 0 n])
xlabel('iteration'), ylabel('number of nonzeros (cardinality)');
legend('log heuristic','l1-norm heuristic','Location','SouthEast')

Finding a sparse feasible point using l1-norm heuristic ... 
Calling SDPT3 4.0: 200 variables, 100 equality constraints
------------------------------------------------------------

 num. of constraints = 100
 dim. of socp   var  = 100,   num. of socp blk  = 50
 dim. of linear var  = 100
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|1.5e+01|1.5e+01|1.3e+05| 2.306427e+02  0.000000e+00| 0:0:00| chol  1  1 
 1|0.607|0.203|5.7e+00|1.2e+01|9.6e+04| 2.372055e+03 -7.798589e+01| 0:0:00| chol  1  1 
 2|0.527|0.755|2.7e+00|3.0e+00|4.4e+04| 2.913698e+03 -4.649185e+02| 0:0:00| chol  1  1 
 3|0.783|1.000|5.9e-01|2.7e-02|1.1e+04| 2.265689e+03 -7.312838e+02| 0:0:00| chol  1  1 
 4|0.933|1.000|3.9e-02|8.1e-03|1.2e+03| 1.752965e+02 -6.105356e+02| 0:0:00| chol  1  1 
 5|1.000|0.960|7.9e-07|8.9e-03|2.8e+02| 1.050573e+02 -1.760406e+02| 0:0:00| chol  1  1 
 6|0.842|0.872|3.2e-07|1.2e-03|5.3e+01| 5.663446e+01  3.546144e+00| 0:0:00| chol  1  1 
 7|0.590|0.753|1.4e-07|3.1e-04|3.3e+01| 4.833162e+01  1.570252e+01| 0:0:00| chol  1  1 
 8|0.864|0.581|2.2e-08|1.3e-04|1.9e+01| 4.206510e+01  2.318715e+01| 0:0:00| chol  1  1 
 9|1.000|0.553|1.2e-09|5.8e-05|1.1e+01| 3.937001e+01  2.867040e+01| 0:0:00| chol  1  1 
10|1.000|0.851|9.8e-14|8.6e-06|3.9e+00| 3.750190e+01  3.356489e+01| 0:0:00| chol  1  1 
11|0.857|0.651|2.1e-14|3.0e-06|2.2e+00| 3.675586e+01  3.455323e+01| 0:0:00| chol  1  1 
12|0.885|1.000|5.3e-14|8.2e-11|1.1e+00| 3.647209e+01  3.541597e+01| 0:0:00| chol  1  1 
13|1.000|0.971|2.8e-14|1.1e-11|2.2e-01| 3.604244e+01  3.581861e+01| 0:0:00| chol  1  1 
14|1.000|0.667|1.3e-12|5.3e-12|9.5e-02| 3.597437e+01  3.587946e+01| 0:0:00| chol  1  1 
15|0.965|0.928|1.5e-12|1.5e-12|1.7e-02| 3.594769e+01  3.593091e+01| 0:0:00| chol  1  1 
16|0.873|1.000|1.4e-12|1.0e-12|5.3e-03| 3.594352e+01  3.593821e+01| 0:0:00| chol  1  2 
17|0.920|0.980|1.7e-12|1.0e-12|5.9e-04| 3.594114e+01  3.594055e+01| 0:0:00| chol  2  2 
18|1.000|0.977|8.1e-12|1.0e-12|5.9e-05| 3.594080e+01  3.594074e+01| 0:0:00| chol  2  2 
19|0.996|0.998|2.0e-12|1.5e-12|9.1e-07| 3.594078e+01  3.594078e+01| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 19
 primal objective value =  3.59407774e+01
 dual   objective value =  3.59407765e+01
 gap := trace(XZ)       = 9.08e-07
 relative gap           = 1.25e-08
 actual relative gap    = 1.25e-08
 rel. primal infeas (scaled problem)   = 2.01e-12
 rel. dual     "        "       "      = 1.50e-12
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 1.7e+01, 1.6e+00, 9.9e+00
 norm(A), norm(b), norm(C) = 7.3e+01, 8.9e+01, 8.1e+00
 Total CPU time (secs)  = 0.29  
 CPU time per iteration = 0.02  
 termination code       =  0
 DIMACS: 6.9e-12  0.0e+00  6.1e-12  0.0e+00  1.2e-08  1.2e-08
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +35.9408
 

Found a feasible x in R^50 that has 46 nonzeros using the l1-norm heuristic.

Log-based heuristic:
   found a solution with 46 nonzeros...
   found a solution with 37 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...
   found a solution with 35 nonzeros...

Found a feasible x in R^50 that has 35 nonzeros using the log heuristic.