FDLA and FMMC solutions for an 8-node, 13-edge graph

Jump to:     Source code     Text output      Plots     Library index

% S. Boyd, et. al., "Convex Optimization of Graph Laplacian Eigenvalues"
% ICM'06 talk examples (www.stanford.edu/~boyd/cvx_opt_graph_lapl_eigs.html)
% Written for CVX by Almir Mutapcic 08/29/06
% (figures are generated)
%
% In this example we consider a graph described by the incidence matrix A.
% Each edge has a weight W_i, and we optimize various functions of the
% edge weights as described in the referenced paper; in particular,
%
% - the fastest distributed linear averaging (FDLA) problem (fdla.m)
% - the fastest mixing Markov chain (FMMC) problem (fmmc.m)
%
% Then we compare these solutions to the heuristics listed below:
%
% - maximum-degree heuristic (max_deg.m)
% - constant weights that yield fastest averaging (best_const.m)
% - Metropolis-Hastings heuristic (mh.m)

% small example (incidence matrix A)
A = [ 1  0  0  1  0  0  0  0  0  0  0  0  0;
     -1  1  0  0  1  1  0  0  0  0  0  0  1;
      0 -1  1  0  0  0  0  0 -1  0  0  0  0;
      0  0 -1  0  0 -1  0  0  0 -1  0  0  0;
      0  0  0 -1  0  0 -1  1  0  0  0  0  0;
      0  0  0  0  0  0  1  0  0  0  1  0  0;
      0  0  0  0  0  0  0 -1  1  0 -1  1 -1;
      0  0  0  0 -1  0  0  0  0  1  0 -1  0];

% x and y locations of the graph nodes
xy = [ 1 2   3 3 1 1 2   3 ; ...
       3 2.5 3 2 2 1 1.5 1 ]';

% Compute edge weights: some optimal, some based on heuristics
[n,m] = size(A);

[ w_fdla, rho_fdla ] = fdla(A);
[ w_fmmc, rho_fmmc ] = fmmc(A);
[ w_md,   rho_md   ] = max_deg(A);
[ w_bc,   rho_bc   ] = best_const(A);
[ w_mh,   rho_mh   ] = mh(A);

tau_fdla = 1/log(1/rho_fdla);
tau_fmmc = 1/log(1/rho_fmmc);
tau_md   = 1/log(1/rho_md);
tau_bc   = 1/log(1/rho_bc);
tau_mh   = 1/log(1/rho_mh);

fprintf(1,'\nResults:\n');
fprintf(1,'FDLA weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fdla,tau_fdla);
fprintf(1,'FMMC weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fmmc,tau_fmmc);
fprintf(1,'M-H weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_mh,tau_mh);
fprintf(1,'MAX_DEG weights:\t rho = %5.4f \t tau = %5.4f\n',rho_md,tau_md);
fprintf(1,'BEST_CONST weights:\t rho = %5.4f \t tau = %5.4f\n',rho_bc,tau_bc);

% Plot results
figure(1), clf
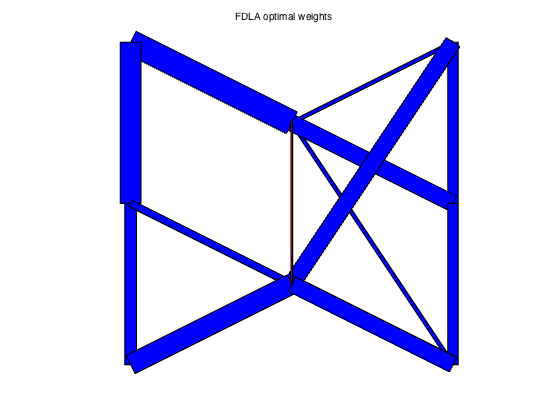
plotgraph(A,xy,w_fdla);
text(0.55,1.05,'FDLA optimal weights')

figure(2), clf
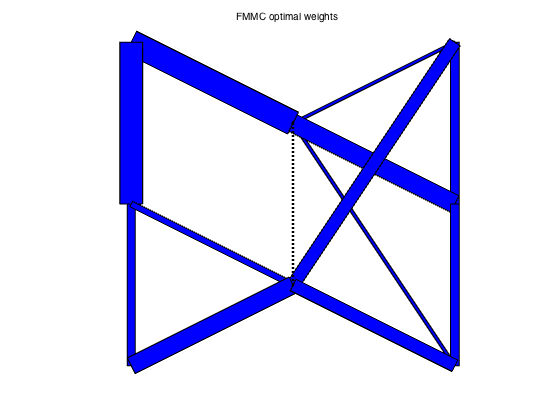
plotgraph(A,xy,w_fmmc);
text(0.55,1.05,'FMMC optimal weights')

figure(3), clf
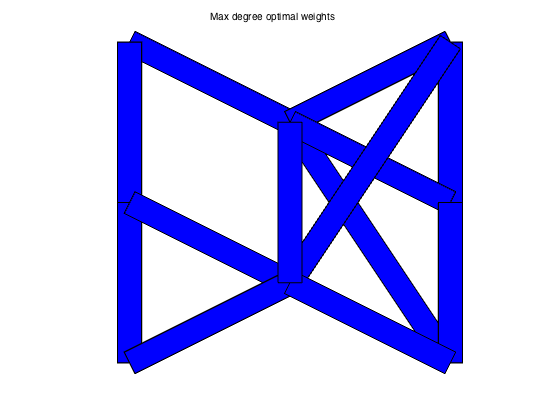
plotgraph(A,xy,w_md);
text(0.5,1.05,'Max degree optimal weights')

figure(4), clf
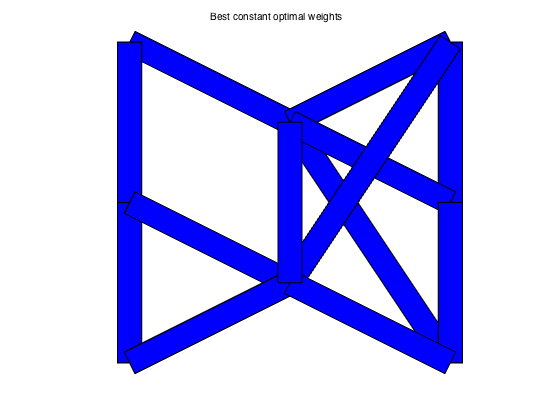
plotgraph(A,xy,w_bc);
text(0.5,1.05,'Best constant optimal weights')

figure(5), clf
plotgraph(A,xy,w_mh);
text(0.46,1.05,'Metropolis-Hastings optimal weights')

 
Calling SDPT3 4.0: 75 variables, 17 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 17
 dim. of sdp    var  = 16,   num. of sdp  blk  =  2
 dim. of free   var  =  3 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|8.0e+01|1.2e+01|1.9e+03|-3.497627e-10  0.000000e+00| 0:0:00| chol  1  1 
 1|0.972|0.990|2.2e+00|2.2e-01|5.4e+01|-1.843757e-01 -9.715678e+00| 0:0:00| chol  1  1 
 2|1.000|1.000|1.0e-05|1.0e-02|6.6e+00|-5.104588e-02 -6.614927e+00| 0:0:00| chol  1  1 
 3|1.000|0.884|3.0e-05|2.0e-03|7.8e-01|-9.619088e-02 -8.750210e-01| 0:0:00| chol  1  1 
 4|0.537|0.052|1.4e-05|2.3e-03|4.5e-01|-4.520340e-01 -8.823194e-01| 0:0:00| chol  1  1 
 5|1.000|0.639|3.5e-07|8.2e-04|1.4e-01|-6.041297e-01 -7.417491e-01| 0:0:00| chol  1  1 
 6|0.968|0.872|1.2e-07|1.1e-04|1.6e-02|-6.397189e-01 -6.555184e-01| 0:0:00| chol  1  1 
 7|0.975|0.665|7.0e-09|3.6e-05|4.5e-03|-6.430462e-01 -6.474730e-01| 0:0:00| chol  1  1 
 8|1.000|0.486|1.3e-09|1.8e-05|2.2e-03|-6.432587e-01 -6.454737e-01| 0:0:00| chol  1  1 
 9|0.997|0.885|2.8e-10|2.1e-06|2.5e-04|-6.433290e-01 -6.435785e-01| 0:0:00| chol  1  1 
10|0.968|0.950|6.3e-11|3.7e-06|1.4e-05|-6.433313e-01 -6.433437e-01| 0:0:00| chol  1  1 
11|1.000|0.967|7.1e-13|2.1e-07|6.9e-07|-6.433313e-01 -6.433319e-01| 0:0:00| chol  1  1 
12|1.000|0.988|2.1e-13|1.0e-08|1.8e-08|-6.433314e-01 -6.433314e-01| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 12
 primal objective value = -6.43331397e-01
 dual   objective value = -6.43331410e-01
 gap := trace(XZ)       = 1.75e-08
 relative gap           = 7.66e-09
 actual relative gap    = 5.62e-09
 rel. primal infeas (scaled problem)   = 2.05e-13
 rel. dual     "        "       "      = 1.02e-08
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 8.3e-01, 1.7e+00, 3.2e+00
 norm(A), norm(b), norm(C) = 1.3e+01, 2.0e+00, 3.8e+00
 Total CPU time (secs)  = 0.22  
 CPU time per iteration = 0.02  
 termination code       =  0
 DIMACS: 2.1e-13  0.0e+00  1.9e-08  0.0e+00  5.6e-09  7.7e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.643331
 
 
Calling SDPT3 4.0: 99 variables, 20 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 20
 dim. of sdp    var  = 16,   num. of sdp  blk  =  2
 dim. of linear var  = 21
 dim. of free   var  =  6 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|8.2e+01|1.9e+01|7.2e+03| 3.125000e+01  0.000000e+00| 0:0:00| chol  1  1 
 1|0.873|0.940|1.0e+01|1.2e+00|4.6e+02| 4.388291e+01 -9.677667e+00| 0:0:00| chol  1  1 
 2|0.984|0.942|1.7e-01|7.9e-02|4.8e+01| 2.886496e+01 -8.898537e+00| 0:0:00| chol  1  1 
 3|0.981|0.409|3.1e-03|4.7e-02|1.2e+01| 3.565300e+00 -6.727515e+00| 0:0:00| chol  1  1 
 4|0.924|0.878|2.3e-04|6.5e-03|1.3e+00| 2.602933e-01 -1.038169e+00| 0:0:00| chol  1  1 
 5|0.412|0.280|1.4e-04|4.7e-03|1.1e+00| 1.753960e-02 -1.022032e+00| 0:0:00| chol  1  1 
 6|1.000|0.237|6.6e-08|3.6e-03|5.6e-01|-4.336242e-01 -9.646712e-01| 0:0:00| chol  1  1 
 7|1.000|0.454|5.1e-08|2.0e-03|3.0e-01|-5.415723e-01 -8.356418e-01| 0:0:00| chol  1  1 
 8|1.000|0.670|1.1e-08|6.5e-04|8.3e-02|-6.489499e-01 -7.298489e-01| 0:0:00| chol  1  1 
 9|1.000|0.506|1.4e-09|3.2e-04|3.2e-02|-6.742301e-01 -7.051268e-01| 0:0:00| chol  1  1 
10|0.917|0.841|1.0e-09|5.1e-05|5.1e-03|-6.797412e-01 -6.847919e-01| 0:0:00| chol  1  1 
11|0.953|0.473|1.6e-10|2.7e-05|2.3e-03|-6.807518e-01 -6.829896e-01| 0:0:00| chol  1  1 
12|0.985|0.966|1.8e-10|2.1e-05|1.0e-04|-6.809546e-01 -6.810312e-01| 0:0:00| chol  1  1 
13|0.955|0.977|8.3e-12|9.1e-07|2.9e-06|-6.809604e-01 -6.809623e-01| 0:0:00| chol  1  1 
14|1.000|0.967|6.9e-14|2.6e-08|1.6e-07|-6.809606e-01 -6.809607e-01| 0:0:00| chol  1  1 
15|1.000|0.985|1.8e-14|1.5e-09|6.0e-09|-6.809607e-01 -6.809607e-01| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 15
 primal objective value = -6.80960673e-01
 dual   objective value = -6.80960677e-01
 gap := trace(XZ)       = 6.05e-09
 relative gap           = 2.56e-09
 actual relative gap    = 1.94e-09
 rel. primal infeas (scaled problem)   = 1.79e-14
 rel. dual     "        "       "      = 1.45e-09
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 1.1e+00, 1.3e+00, 3.6e+00
 norm(A), norm(b), norm(C) = 1.4e+01, 2.0e+00, 3.9e+00
 Total CPU time (secs)  = 0.30  
 CPU time per iteration = 0.02  
 termination code       =  0
 DIMACS: 1.8e-14  0.0e+00  3.1e-09  0.0e+00  1.9e-09  2.6e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.680961
 

Results:
FDLA weights:		 rho = 0.6433 	 tau = 2.2671
FMMC weights:		 rho = 0.6810 	 tau = 2.6025
M-H weights:		 rho = 0.7743 	 tau = 3.9094
MAX_DEG weights:	 rho = 0.7793 	 tau = 4.0093
BEST_CONST weights:	 rho = 0.7119 	 tau = 2.9422