FDLA and FMMC solutions for a 64-node, 95-edge cut-grid graph

Jump to:     Source code     Text output      Plots     Library index

% S. Boyd, et. al., "Convex Optimization of Graph Laplacian Eigenvalues"
% ICM'06 talk examples (www.stanford.edu/~boyd/cvx_opt_graph_lapl_eigs.html)
% Written for CVX by Almir Mutapcic 08/29/06
% (figures are generated)
%
% In this example we consider a graph described by the incidence matrix A.
% Each edge has a weight W_i, and we optimize various functions of the
% edge weights as described in the referenced paper; in particular,
%
% - the fastest distributed linear averaging (FDLA) problem (fdla.m)
% - the fastest mixing Markov chain (FMMC) problem (fmmc.m)
%
% Then we compare these solutions to the heuristics listed below:
%
% - maximum-degree heuristic (max_deg.m)
% - constant weights that yield fastest averaging (best_const.m)
% - Metropolis-Hastings heuristic (mh.m)

% generate a cut-grid graph example
[A,xy] = cut_grid_data;

% Compute edge weights: some optimal, some based on heuristics
[n,m] = size(A);

[ w_fdla, rho_fdla ] = fdla(A);
[ w_fmmc, rho_fmmc ] = fmmc(A);
[ w_md,   rho_md   ] = max_deg(A);
[ w_bc,   rho_bc   ] = best_const(A);
[ w_mh,   rho_mh   ] = mh(A);

tau_fdla = 1/log(1/rho_fdla);
tau_fmmc = 1/log(1/rho_fmmc);
tau_md   = 1/log(1/rho_md);
tau_bc   = 1/log(1/rho_bc);
tau_mh   = 1/log(1/rho_mh);

fprintf(1,'\nResults:\n');
fprintf(1,'FDLA weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fdla,tau_fdla);
fprintf(1,'FMMC weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fmmc,tau_fmmc);
fprintf(1,'M-H weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_mh,tau_mh);
fprintf(1,'MAX_DEG weights:\t rho = %5.4f \t tau = %5.4f\n',rho_md,tau_md);
fprintf(1,'BEST_CONST weights:\t rho = %5.4f \t tau = %5.4f\n',rho_bc,tau_bc);

% plot results
figure(1), clf
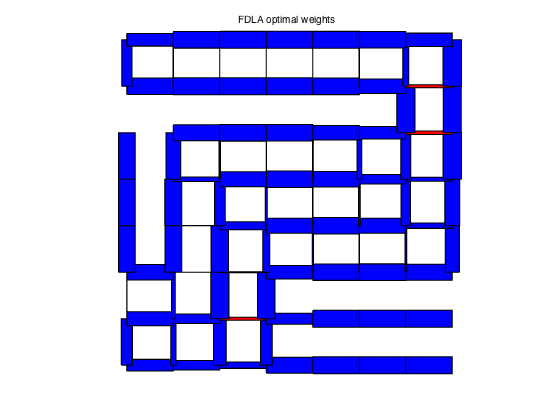
plotgraph(A,xy,w_fdla);
text(0.425,1.05,'FDLA optimal weights')

figure(2), clf
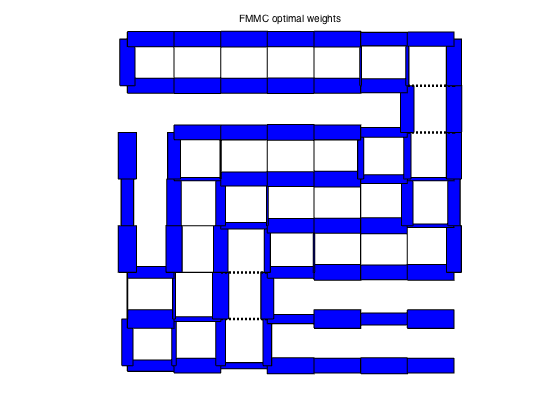
plotgraph(A,xy,w_fmmc);
text(0.425,1.05,'FMMC optimal weights')

figure(3), clf
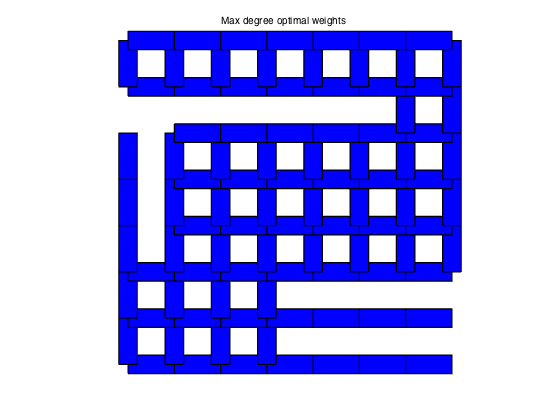
plotgraph(A,xy,w_md);
text(0.375,1.05,'Max degree optimal weights')

figure(4), clf
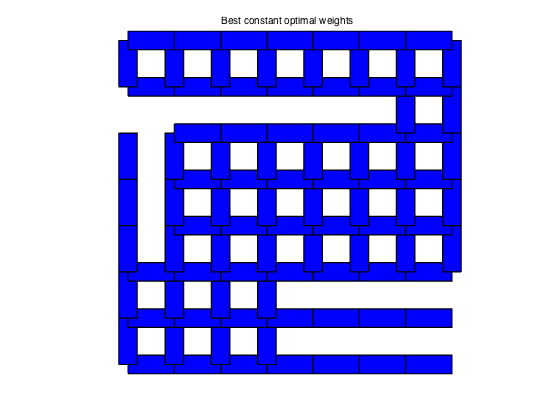
plotgraph(A,xy,w_bc);
text(0.375,1.05,'Best constant optimal weights')

figure(5), clf
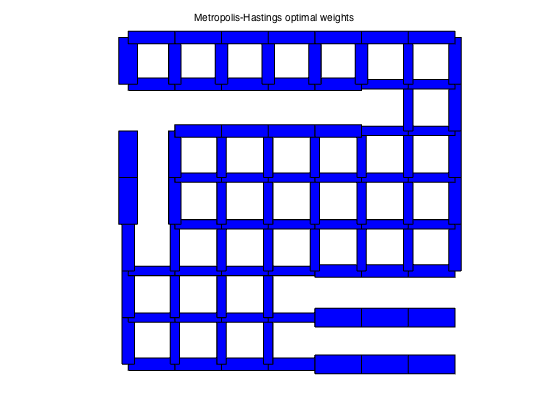
plotgraph(A,xy,w_mh);
text(0.3,1.05,'Metropolis-Hastings optimal weights')

 
Calling SDPT3 4.0: 4184 variables, 120 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 120
 dim. of sdp    var  = 128,   num. of sdp  blk  =  2
 dim. of free   var  = 24 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|2.0e+03|3.4e+01|1.7e+05| 1.089011e-08  0.000000e+00| 0:0:00| chol  1  1 
 1|0.895|0.972|2.2e+02|1.0e+00|5.8e+03|-1.756578e+01 -1.110230e+01| 0:0:00| chol  1  1 
 2|0.978|0.983|4.7e+00|2.6e-02|1.2e+02|-2.214736e-01 -1.144711e+01| 0:0:00| chol  1  1 
 3|1.000|1.000|1.2e-04|1.0e-03|9.3e+00|-4.791766e-02 -9.366149e+00| 0:0:00| chol  2  1 
 4|1.000|0.890|4.6e-04|2.2e-04|1.0e+00|-1.061429e-01 -1.155671e+00| 0:0:00| chol  1  1 
 5|0.793|0.033|9.4e-05|2.8e-04|4.3e-01|-7.675579e-01 -1.161431e+00| 0:0:00| chol  1  1 
 6|1.000|0.735|8.0e-06|9.4e-05|1.4e-01|-8.890822e-01 -1.028414e+00| 0:0:00| chol  1  1 
 7|0.968|0.487|1.2e-06|5.0e-05|5.8e-02|-9.509494e-01 -1.006792e+00| 0:0:00| chol  1  2 
 8|0.895|0.581|4.6e-07|2.1e-05|1.8e-02|-9.780891e-01 -9.957371e-01| 0:0:00| chol  2  2 
 9|0.934|0.361|1.2e-07|1.4e-05|8.6e-03|-9.846282e-01 -9.930642e-01| 0:0:00| chol  2  2 
10|1.000|0.407|4.5e-08|1.6e-05|4.5e-03|-9.868529e-01 -9.911189e-01| 0:0:00| chol  1  2 
11|1.000|0.904|2.9e-09|7.5e-06|5.5e-04|-9.880224e-01 -9.885365e-01| 0:0:00| chol  1  1 
12|0.968|0.959|1.7e-10|9.2e-07|1.2e-04|-9.881921e-01 -9.883072e-01| 0:0:00| chol  1  1 
13|1.000|0.977|5.1e-11|1.9e-07|1.3e-05|-9.882804e-01 -9.882927e-01| 0:0:01| chol  1  1 
14|1.000|0.980|6.9e-11|2.1e-08|7.6e-07|-9.882912e-01 -9.882919e-01| 0:0:01| chol  2  2 
15|1.000|0.986|1.6e-11|1.3e-09|2.7e-08|-9.882919e-01 -9.882919e-01| 0:0:01|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 15
 primal objective value = -9.88291858e-01
 dual   objective value = -9.88291885e-01
 gap := trace(XZ)       = 2.72e-08
 relative gap           = 9.13e-09
 actual relative gap    = 8.86e-09
 rel. primal infeas (scaled problem)   = 1.64e-11
 rel. dual     "        "       "      = 1.26e-09
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 9.9e-01, 6.6e+00, 1.3e+01
 norm(A), norm(b), norm(C) = 3.5e+01, 2.0e+00, 1.2e+01
 Total CPU time (secs)  = 0.62  
 CPU time per iteration = 0.04  
 termination code       =  0
 DIMACS: 1.6e-11  0.0e+00  7.6e-09  0.0e+00  8.9e-09  9.1e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.988292
 
 
Calling SDPT3 4.0: 4366 variables, 143 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 143
 dim. of sdp    var  = 128,   num. of sdp  blk  =  2
 dim. of linear var  = 159
 dim. of free   var  = 47 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|2.1e+03|7.8e+01|1.8e+06| 4.543368e+02  0.000000e+00| 0:0:00| chol  1  1 
 1|0.792|0.933|4.3e+02|5.4e+00|4.2e+04| 8.746282e+02 -1.017808e+01| 0:0:00| chol  1  1 
 2|0.894|0.971|4.5e+01|2.2e-01|2.3e+03| 7.232508e+02 -1.051730e+01| 0:0:00| chol  1  1 
 3|0.943|0.889|2.6e+00|3.2e-02|2.0e+02| 1.138259e+02 -1.091175e+01| 0:0:00| chol  1  1 
 4|0.996|0.762|9.9e-03|8.3e-03|1.7e+01| 6.171218e+00 -9.192581e+00| 0:0:00| chol  1  1 
 5|0.958|0.889|4.1e-04|2.9e-03|1.4e+00| 1.602182e-01 -1.159879e+00| 0:0:00| chol  1  1 
 6|0.532|0.514|1.9e-04|1.5e-03|9.9e-01|-2.051199e-01 -1.170932e+00| 0:0:00| chol  1  1 
 7|1.000|0.329|3.9e-08|1.1e-03|3.5e-01|-7.741474e-01 -1.114688e+00| 0:0:00| chol  1  1 
 8|1.000|0.544|2.5e-08|4.8e-04|1.3e-01|-9.079432e-01 -1.037562e+00| 0:0:00| chol  1  1 
 9|0.937|0.465|8.7e-09|2.6e-04|5.8e-02|-9.549590e-01 -1.011399e+00| 0:0:00| chol  1  1 
10|0.839|0.405|3.4e-09|1.5e-04|2.8e-02|-9.745663e-01 -1.001890e+00| 0:0:00| chol  1  1 
11|0.897|0.342|1.3e-09|9.4e-05|1.5e-02|-9.826287e-01 -9.976444e-01| 0:0:01| chol  1  1 
12|0.946|0.945|4.5e-10|1.6e-05|3.6e-03|-9.861534e-01 -9.896009e-01| 0:0:01| chol  1  1 
13|0.937|0.935|7.3e-11|3.6e-06|1.5e-03|-9.876189e-01 -9.891192e-01| 0:0:01| chol  2  2 
14|0.907|0.888|1.2e-10|1.5e-06|3.7e-04|-9.885403e-01 -9.888995e-01| 0:0:01| chol  2  2 
15|0.938|0.933|6.5e-11|3.7e-07|1.8e-04|-9.886851e-01 -9.888664e-01| 0:0:01| chol  2  2 
16|1.000|0.949|7.7e-10|1.9e-07|6.2e-05|-9.887810e-01 -9.888403e-01| 0:0:01| chol  2  2 
17|1.000|0.958|3.7e-10|6.2e-08|1.7e-05|-9.888136e-01 -9.888302e-01| 0:0:01| chol  2  2 
18|1.000|0.959|1.1e-10|1.7e-08|4.5e-06|-9.888228e-01 -9.888272e-01| 0:0:01| chol  2  2 
19|1.000|0.959|9.8e-11|4.6e-09|1.2e-06|-9.888253e-01 -9.888264e-01| 0:0:01| chol  3  4 
20|1.000|0.956|7.2e-10|1.3e-09|3.7e-07|-9.888259e-01 -9.888262e-01| 0:0:01| chol  4  6 
21|1.000|0.958|8.7e-10|3.9e-10|1.0e-07|-9.888261e-01 -9.888262e-01| 0:0:01| chol  6  7 
22|1.000|0.955|4.4e-10|1.3e-10|3.1e-08|-9.888261e-01 -9.888262e-01| 0:0:01|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 22
 primal objective value = -9.88826133e-01
 dual   objective value = -9.88826162e-01
 gap := trace(XZ)       = 3.08e-08
 relative gap           = 1.03e-08
 actual relative gap    = 9.80e-09
 rel. primal infeas (scaled problem)   = 4.36e-10
 rel. dual     "        "       "      = 1.32e-10
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 1.0e+00, 3.8e+00, 1.4e+01
 norm(A), norm(b), norm(C) = 3.6e+01, 2.0e+00, 1.3e+01
 Total CPU time (secs)  = 1.01  
 CPU time per iteration = 0.05  
 termination code       =  0
 DIMACS: 4.4e-10  0.0e+00  8.4e-10  0.0e+00  9.8e-09  1.0e-08
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.988826
 

Results:
FDLA weights:		 rho = 0.9883 	 tau = 84.9099
FMMC weights:		 rho = 0.9888 	 tau = 88.9938
M-H weights:		 rho = 0.9917 	 tau = 120.2442
MAX_DEG weights:	 rho = 0.9927 	 tau = 136.7523
BEST_CONST weights:	 rho = 0.9921 	 tau = 126.3450