% Section 8.6.1, Boyd & Vandenberghe "Convex Optimization"
% Original by Lieven Vandenberghe
% Adapted for CVX by Joelle Skaf - 10/16/05
% (a figure is generated)
%
% The goal is to find a function f(x) = a'*x - b that classifies the non-
% separable points {x_1,...,x_N} and {y_1,...,y_M} by doing a trade-off
% between the number of misclassifications and the width of the separating
% slab. a and b can be obtained by solving the following problem:
%           minimize    ||a||_2 + gamma*(1'*u + 1'*v)
%               s.t.    a'*x_i - b >= 1 - u_i        for i = 1,...,N
%                       a'*y_i - b <= -(1 - v_i)     for i = 1,...,M
%                       u >= 0 and v >= 0
% where gamma gives the relative weight of the number of misclassified
% points compared to the width of the slab.

% data generation
n = 2;
randn('state',2);
N = 50; M = 50;
Y = [1.5+0.9*randn(1,0.6*N), 1.5+0.7*randn(1,0.4*N);
     2*(randn(1,0.6*N)+1), 2*(randn(1,0.4*N)-1)];
X = [-1.5+0.9*randn(1,0.6*M),  -1.5+0.7*randn(1,0.4*M);
      2*(randn(1,0.6*M)-1), 2*(randn(1,0.4*M)+1)];
T = [-1 1; 1 1];
Y = T*Y;  X = T*X;
g = 0.1;            % gamma

% Solution via CVX
cvx_begin
    variables a(n) b(1) u(N) v(M)
    minimize (norm(a) + g*(ones(1,N)*u + ones(1,M)*v))
    X'*a - b >= 1 - u;
    Y'*a - b <= -(1 - v);
    u >= 0;
    v >= 0;
cvx_end

% Displaying results
linewidth = 0.5;  % for the squares and circles
t_min = min([X(1,:),Y(1,:)]);
t_max = max([X(1,:),Y(1,:)]);
tt = linspace(t_min-1,t_max+1,100);
p = -a(1)*tt/a(2) + b/a(2);
p1 = -a(1)*tt/a(2) + (b+1)/a(2);
p2 = -a(1)*tt/a(2) + (b-1)/a(2);

graph = plot(X(1,:),X(2,:), 'o', Y(1,:), Y(2,:), 'o');
set(graph(1),'LineWidth',linewidth);
set(graph(2),'LineWidth',linewidth);
set(graph(2),'MarkerFaceColor',[0 0.5 0]);
hold on;
plot(tt,p, '-r', tt,p1, '--r', tt,p2, '--r');
axis equal
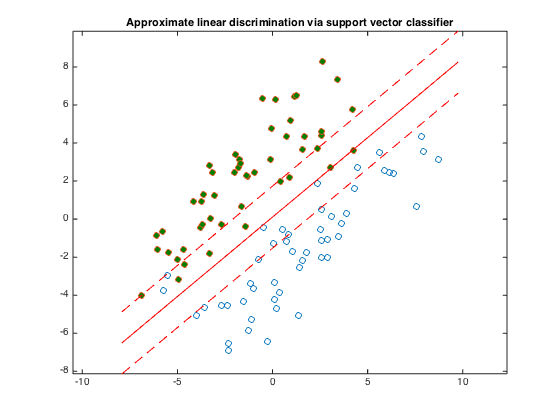
title('Approximate linear discrimination via support vector classifier');
% print -deps svc-discr2.eps

 
Calling SDPT3 4.0: 204 variables, 100 equality constraints
------------------------------------------------------------

 num. of constraints = 100
 dim. of socp   var  =  3,   num. of socp blk  =  1
 dim. of linear var  = 200
 dim. of free   var  =  1 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|9.1e-01|8.3e+01|4.0e+04| 1.435458e+02  0.000000e+00| 0:0:00| chol  1  1 
 1|1.000|0.982|8.8e-08|1.6e+00|8.9e+02| 1.425358e+02  1.331723e+00| 0:0:00| chol  1  1 
 2|1.000|0.565|1.0e-07|6.9e-01|3.7e+02| 9.529609e+01  1.477846e+00| 0:0:00| chol  1  1 
 3|1.000|0.164|3.9e-07|5.8e-01|2.8e+02| 6.293819e+01  1.440057e+00| 0:0:00| chol  1  1 
 4|1.000|0.836|2.2e-07|9.5e-02|5.5e+01| 2.760459e+01  1.192363e+00| 0:0:00| chol  1  1 
 5|0.937|0.799|2.8e-08|1.9e-02|9.8e+00| 7.384521e+00  1.062058e+00| 0:0:00| chol  1  1 
 6|1.000|0.164|5.4e-08|1.6e-02|5.4e+00| 5.109728e+00  1.100383e+00| 0:0:00| chol  1  1 
 7|1.000|0.421|1.2e-08|9.2e-03|3.0e+00| 3.756532e+00  1.239469e+00| 0:0:00| chol  1  1 
 8|1.000|0.383|4.3e-09|5.7e-03|1.6e+00| 2.728459e+00  1.332853e+00| 0:0:00| chol  1  1 
 9|1.000|0.319|1.5e-09|3.9e-03|1.2e+00| 2.497279e+00  1.448720e+00| 0:0:00| chol  1  1 
10|0.974|0.430|6.0e-10|2.2e-03|6.2e-01| 2.109819e+00  1.542722e+00| 0:0:00| chol  1  1 
11|1.000|0.266|1.3e-10|1.6e-03|5.5e-01| 2.109294e+00  1.601086e+00| 0:0:00| chol  1  1 
12|0.807|0.330|8.8e-11|1.1e-03|4.0e-01| 2.010704e+00  1.636742e+00| 0:0:00| chol  1  1 
13|1.000|0.279|7.6e-11|7.8e-04|3.0e-01| 1.951053e+00  1.668699e+00| 0:0:00| chol  1  1 
14|1.000|0.363|8.3e-11|5.0e-04|2.1e-01| 1.903685e+00  1.707380e+00| 0:0:00| chol  1  1 
15|1.000|0.379|1.8e-11|3.1e-04|1.3e-01| 1.865529e+00  1.741217e+00| 0:0:00| chol  1  1 
16|1.000|0.433|2.0e-11|1.8e-04|7.4e-02| 1.843174e+00  1.772015e+00| 0:0:00| chol  1  1 
17|1.000|0.661|1.5e-11|5.9e-05|2.3e-02| 1.828356e+00  1.806159e+00| 0:0:00| chol  1  1 
18|0.974|0.948|3.0e-12|3.1e-06|1.2e-03| 1.825797e+00  1.824667e+00| 0:0:00| chol  1  2 
19|0.932|0.452|1.8e-11|2.4e-06|6.5e-04| 1.825736e+00  1.825121e+00| 0:0:00| chol  1  2 
20|1.000|0.952|5.0e-12|9.3e-07|1.7e-04| 1.825775e+00  1.825606e+00| 0:0:00| chol  2  1 
21|0.933|0.949|3.0e-12|2.4e-07|5.4e-05| 1.825728e+00  1.825673e+00| 0:0:00| chol  2  2 
22|1.000|0.985|4.1e-11|7.8e-08|2.5e-06| 1.825701e+00  1.825699e+00| 0:0:00| chol  2  1 
23|1.000|0.988|4.4e-11|3.6e-09|6.5e-08| 1.825700e+00  1.825700e+00| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 23
 primal objective value =  1.82570024e+00
 dual   objective value =  1.82570018e+00
 gap := trace(XZ)       = 6.50e-08
 relative gap           = 1.40e-08
 actual relative gap    = 1.39e-08
 rel. primal infeas (scaled problem)   = 4.40e-11
 rel. dual     "        "       "      = 3.57e-09
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 1.3e+01, 4.2e-01, 1.7e+00
 norm(A), norm(b), norm(C) = 5.4e+01, 1.1e+01, 2.4e+00
 Total CPU time (secs)  = 0.33  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 2.4e-10  0.0e+00  4.3e-09  0.0e+00  1.4e-08  1.4e-08
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +1.8257