% Section 8.6.2, Boyd & Vandenberghe "Convex Optimization"
% Original by Lieven Vandenberghe
% Adapted for CVX by Joelle Skaf - 10/23/05
% (a figure is generated)
%
% The goal is to find the polynomial of degree 3 on R^n that separates
% two sets of points {x_1,...,x_N} and {y_1,...,y_N}. We are trying to find
% the coefficients of an order-3-polynomial P(x) that would satisfy:
%           minimize    t
%               s.t.    P(x_i) <= t  for i = 1,...,N
%                       P(y_i) >= t   for i = 1,...,M

% Data generation
rand('state',0);
N = 100;
M = 120;

% The points X lie within a circle of radius 0.9, with a wedge of points
% near [1.1,0] removed. The points Y lie outside a circle of radius 1.1,
% with a wedge of points near [1.1,0] added. The wedges are precisely what
% makes the separation difficult and interesting.
X = 2 * rand(2,N) - 1;
X = X * diag(0.9*rand(1,N)./sqrt(sum(X.^2)));
Y = 2 * rand(2,M) - 1;
Y = Y * diag((1.1+rand(1,M))./sqrt(sum(Y.^2)));
d = sqrt(sum((X-[1.1;0]*ones(1,N)).^2));
Y = [ Y, X(:,d<0.9) ];
X = X(:,d>1);
N = size(X,2);
M = size(Y,2);

% Construct Vandermonde-style monomial matrices
p1   = [0,0,1,0,1,2,0,1,2,3]';
p2   = [0,1,1,2,2,2,3,3,3,3]'-p1;
np   = length(p1);
op   = ones(np,1);
monX = X(op,:) .^ p1(:,ones(1,N)) .* X(2*op,:) .^ p2(:,ones(1,N));
monY = Y(op,:) .^ p1(:,ones(1,M)) .* Y(2*op,:) .^ p2(:,ones(1,M));

% Solution via CVX
fprintf(1,'Finding the optimal polynomial of order 4 that separates the 2 classes...');

cvx_begin
    variables a(np) t(1)
    minimize ( t )
    a'*monX <= t;
    a'*monY >= -t;
cvx_end

fprintf(1,'Done! \n');

% Displaying results
nopts = 2000;
angles = linspace(0,2*pi,nopts);
cont = zeros(2,nopts);
for i=1:nopts
   v = [cos(angles(i)); sin(angles(i))];
   l = 0;  u = 1;
   while ( u - l > 1e-3 )
      s = (u+l)/2;
      x = s * v;
      if a' * ( x(op,:) .^ p1 .* x(2*op) .^ p2 ) > 0,
          u = s;
      else
          l = s;
      end
   end;
   s = (u+l)/2;
   cont(:,i) = s*v;
end;

graph=plot(X(1,:),X(2,:),'o', Y(1,:), Y(2,:),'o', cont(1,:), cont(2,:), '-');
set(graph(2),'MarkerFaceColor',[0 0.5 0]);
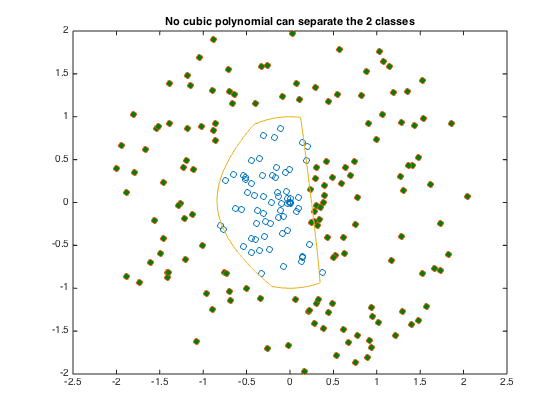
title('No cubic polynomial can separate the 2 classes')

% Results
disp('-----------------------------------------------------------------');
disp('As seen on the figure, the 2 sets of points are not separated.   ');
disp('There exists no cubic polynomial that can separate these 2 sets.');

Finding the optimal polynomial of order 4 that separates the 2 classes... 
Calling SDPT3 4.0: 211 variables, 11 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 11
 dim. of linear var  = 211
 number of nearly dependent constraints = 1
 To remove these constraints, re-run sqlp.m with OPTIONS.rmdepconstr = 1.
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|2.3e+03|4.5e+02|9.5e+04| 0.000000e+00  0.000000e+00| 0:0:00| chol  1  1 
 1|0.988|1.000|2.8e+01|1.0e-01|1.2e+03| 0.000000e+00 -3.090416e+01| 0:0:00| chol  1  1 
 2|0.908|1.000|2.5e+00|1.0e-02|1.3e+02| 0.000000e+00 -2.722116e+01| 0:0:00| chol  1  1 
 3|0.619|1.000|9.7e-01|1.0e-03|6.3e+01| 0.000000e+00 -1.212424e+01| 0:0:00| chol  1  1 
 4|0.557|0.632|4.3e-01|4.3e-04|3.8e+01| 0.000000e+00 -9.406926e+00| 0:0:00| chol  1  1 
 5|0.469|0.985|2.3e-01|1.6e-05|2.7e+01| 0.000000e+00 -7.221409e+00| 0:0:00| chol  1  1 
 6|0.823|0.929|4.0e-02|2.1e-06|7.1e+00| 0.000000e+00 -3.487094e+00| 0:0:00| chol  1  1 
 7|0.692|0.874|1.2e-02|8.1e-03|3.2e+00| 0.000000e+00 -2.263036e+00| 0:0:00| chol  1  1 
 8|1.000|1.000|5.3e-09|2.5e-03|1.2e+00| 0.000000e+00 -1.170978e+00| 0:0:00| chol  1  1 
 9|1.000|0.989|7.7e-09|2.7e-05|1.3e-02| 0.000000e+00 -1.276450e-02| 0:0:00| chol  1  1 
10|1.000|0.989|2.6e-09|3.0e-07|1.4e-04| 0.000000e+00 -1.402726e-04| 0:0:00| chol  1  1 
11|1.000|0.994|8.5e-10|2.3e-09|2.4e-06| 0.000000e+00 -2.363420e-06| 0:0:00| chol  1  1 
12|1.000|0.996|3.2e-10|1.8e-10|3.4e-08| 0.000000e+00 -3.357364e-08| 0:0:00| chol  1  1 
13|1.000|0.998|3.4e-11|6.5e-11|4.1e-10| 0.000000e+00 -4.092923e-10| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 13
 primal objective value =  0.00000000e+00
 dual   objective value = -4.09292311e-10
 gap := trace(XZ)       = 4.14e-10
 relative gap           = 4.14e-10
 actual relative gap    = 4.09e-10
 rel. primal infeas (scaled problem)   = 3.36e-11
 rel. dual     "        "       "      = 6.48e-11
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 4.8e-01, 1.9e-08, 3.0e-07
 norm(A), norm(b), norm(C) = 6.2e+01, 2.0e+00, 1.0e+00
 Total CPU time (secs)  = 0.10  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 3.4e-11  0.0e+00  6.5e-11  0.0e+00  4.1e-10  4.1e-10
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +4.09292e-10
 
Done! 
-----------------------------------------------------------------
As seen on the figure, the 2 sets of points are not separated.   
There exists no cubic polynomial that can separate these 2 sets.