% Section 8.7.3, Boyd & Vandenberghe "Convex Optimization"
% Original by Lieven Vandenberghe
% Adapted for CVX by Joelle Skaf - 10/24/05
% (a figure is generated)
%
% Placement problem with 6 free points, 8 fixed points and 27 links.
% The coordinates of the free points minimize the sum of the squares of
% Euclidean lengths of the links, i.e.
%           minimize    sum_{i<j) h(||x_i - x_j||)
% where h(z) = z^2.

linewidth = 1;      % in points;  width of dotted lines
markersize = 5;    % in points;  marker size

% Input data
fixed = [ 1   1  -1 -1    1   -1  -0.2  0.1; % coordinates of fixed points
          1  -1  -1  1 -0.5 -0.2    -1    1]';
M = size(fixed,1);  % number of fixed points
N = 6;              % number of free points

% first N columns of A correspond to free points,
% last M columns correspond to fixed points

A = [ 1  0  0 -1  0  0    0  0  0  0  0  0  0  0
      1  0 -1  0  0  0    0  0  0  0  0  0  0  0
      1  0  0  0 -1  0    0  0  0  0  0  0  0  0
      1  0  0  0  0  0   -1  0  0  0  0  0  0  0
      1  0  0  0  0  0    0 -1  0  0  0  0  0  0
      1  0  0  0  0  0    0  0  0  0 -1  0  0  0
      1  0  0  0  0  0    0  0  0  0  0  0  0 -1
      0  1 -1  0  0  0    0  0  0  0  0  0  0  0
      0  1  0 -1  0  0    0  0  0  0  0  0  0  0
      0  1  0  0  0 -1    0  0  0  0  0  0  0  0
      0  1  0  0  0  0    0 -1  0  0  0  0  0  0
      0  1  0  0  0  0    0  0 -1  0  0  0  0  0
      0  1  0  0  0  0    0  0  0  0  0  0 -1  0
      0  0  1 -1  0  0    0  0  0  0  0  0  0  0
      0  0  1  0  0  0    0 -1  0  0  0  0  0  0
      0  0  1  0  0  0    0  0  0  0 -1  0  0  0
      0  0  0  1 -1  0    0  0  0  0  0  0  0  0
      0  0  0  1  0  0    0  0 -1  0  0  0  0  0
      0  0  0  1  0  0    0  0  0 -1  0  0  0  0
      0  0  0  1  0  0    0  0  0  0  0 -1  0  0
      0  0  0  1  0 -1    0  0  0  0  0 -1  0  0        % error in data!!!
      0  0  0  0  1 -1    0  0  0  0  0  0  0  0
      0  0  0  0  1  0   -1  0  0  0  0  0  0  0
      0  0  0  0  1  0    0  0  0 -1  0  0  0  0
      0  0  0  0  1  0    0  0  0  0  0  0  0 -1
      0  0  0  0  0  1    0  0 -1  0  0  0  0  0
      0  0  0  0  0  1    0  0  0  0 -1  0  0  0 ];
nolinks = size(A,1);    % number of links

fprintf(1,'Computing the optimal locations of the 6 free points...');

cvx_begin
    variable x(N+M,2)
    minimize ( sum(square_pos(norms( A*x,2,2 ))))
    x(N+[1:M],:) == fixed;
cvx_end

fprintf(1,'Done! \n');

% Plots
free_sum = x(1:N,:);
figure(1);
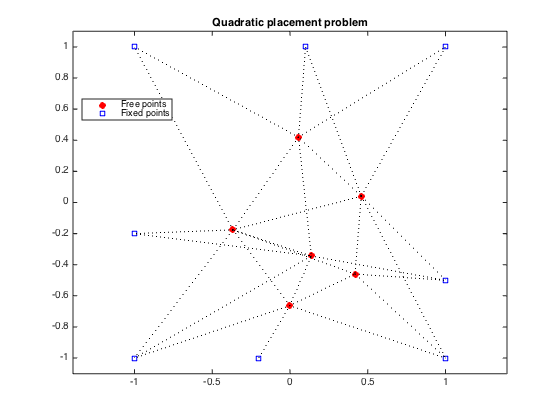
dots = plot(free_sum(:,1), free_sum(:,2), 'or', fixed(:,1), fixed(:,2), 'bs');
set(dots(1),'MarkerFaceColor','red');
hold on
legend('Free points','Fixed points','Location','Best');
for i=1:nolinks
  ind = find(A(i,:));
  line2 = plot(x(ind,1), x(ind,2), ':k');
  hold on
  set(line2,'LineWidth',linewidth);
end
axis([-1.1 1.1 -1.1 1.1]) ;
axis equal;
title('Quadratic placement problem');
% print -deps placement-quadr.eps

figure(2)
all = [free_sum; fixed];
bins = 0.05:0.1:1.95;
lengths = sqrt(sum((A*all).^2')');
[N2,hist2] = hist(lengths,bins);
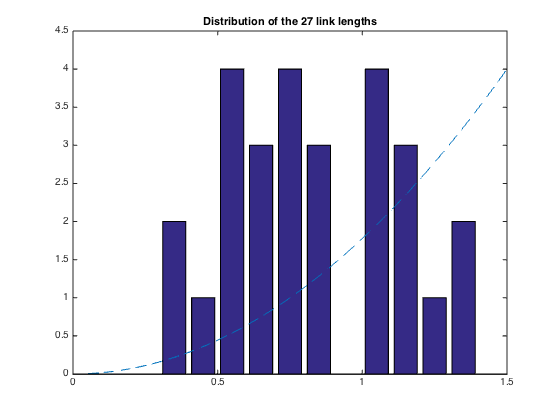
bar(hist2,N2);
hold on;
xx = linspace(0,2,1000); yy = (4/1.5^2)*xx.^2;
plot(xx,yy,'--');
axis([0 1.5 0 4.5]);
hold on
plot([0 2], [0 0 ], 'k-');
title('Distribution of the 27 link lengths');
% print -deps placement-quadr-hist.eps

Computing the optimal locations of the 6 free points... 
Calling SDPT3 4.0: 216 variables, 96 equality constraints
------------------------------------------------------------

 num. of constraints = 96
 dim. of sdp    var  = 54,   num. of sdp  blk  = 27
 dim. of socp   var  = 81,   num. of socp blk  = 27
 dim. of linear var  = 54
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|2.3e+01|1.7e+01|1.8e+04| 2.700000e+02  0.000000e+00| 0:0:00| chol  1  1 
 1|0.692|0.782|7.2e+00|3.7e+00|7.1e+03| 3.503082e+02 -2.313201e+02| 0:0:00| chol  1  1 
 2|0.864|1.000|9.8e-01|1.0e-02|1.5e+03| 6.040152e+02 -3.577982e+02| 0:0:00| chol  1  1 
 3|1.000|1.000|6.5e-07|1.0e-03|3.4e+02| 2.022813e+02 -1.422784e+02| 0:0:00| chol  1  1 
 4|1.000|1.000|7.8e-08|1.0e-04|6.7e+01| 5.801620e+01 -8.700461e+00| 0:0:00| chol  1  1 
 5|1.000|1.000|1.7e-09|1.0e-05|1.5e+01| 3.119476e+01  1.668938e+01| 0:0:00| chol  1  1 
 6|0.904|1.000|5.5e-10|1.0e-06|2.3e+00| 2.233983e+01  2.006406e+01| 0:0:00| chol  1  1 
 7|0.990|0.970|4.8e-10|1.3e-07|2.4e-01| 2.070777e+01  2.047172e+01| 0:0:00| chol  1  1 
 8|0.972|0.970|2.1e-10|1.4e-08|7.6e-03| 2.055233e+01  2.054477e+01| 0:0:00| chol  1  1 
 9|0.973|0.971|2.1e-10|1.4e-09|2.1e-04| 2.054745e+01  2.054724e+01| 0:0:00| chol  1  1 
10|0.911|0.949|1.8e-11|1.1e-10|1.6e-05| 2.054733e+01  2.054731e+01| 0:0:00| chol  1  2 
11|1.000|1.000|3.4e-13|3.7e-12|2.7e-06| 2.054732e+01  2.054731e+01| 0:0:00| chol  1  1 
12|1.000|0.998|1.3e-11|1.0e-12|5.3e-08| 2.054731e+01  2.054731e+01| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 12
 primal objective value =  2.05473136e+01
 dual   objective value =  2.05473136e+01
 gap := trace(XZ)       = 5.28e-08
 relative gap           = 1.25e-09
 actual relative gap    = 1.26e-09
 rel. primal infeas (scaled problem)   = 1.26e-11
 rel. dual     "        "       "      = 1.01e-12
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 1.1e+01, 1.3e+01, 2.0e+01
 norm(A), norm(b), norm(C) = 1.6e+01, 1.1e+01, 6.2e+00
 Total CPU time (secs)  = 0.25  
 CPU time per iteration = 0.02  
 termination code       =  0
 DIMACS: 4.5e-11  0.0e+00  3.1e-12  0.0e+00  1.3e-09  1.3e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +20.5473
 
Done!