% Boyd & Vandenberghe "Convex Optimization"
% Joelle Skaf - 10/16/05
% (a figure is generated)
%
% The goal is to find a function f(x) = a'*x - b that classifies the points
% {x_1,...,x_N} and {y_1,...,y_M}. a and b can be obtained by solving a
% feasibility problem:
%           minimize    0
%               s.t.    a'*x_i - b >=  1     for i = 1,...,N
%                       a'*y_i - b <= -1     for i = 1,...,M

% data generation
n = 2;
randn('state',3);
N = 10; M = 6;
Y = [1.5+1*randn(1,M); 2*randn(1,M)];
X = [-1.5+1*randn(1,N); 2*randn(1,N)];
T = [-1 1; 1 1];
Y = T*Y;  X = T*X;

% Solution via CVX
fprintf('Finding a separating hyperplane...');

cvx_begin
    variables a(n) b(1)
    X'*a - b >= 1;
    Y'*a - b <= -1;
cvx_end

fprintf(1,'Done! \n');

% Displaying results
linewidth = 0.5;  % for the squares and circles
t_min = min([X(1,:),Y(1,:)]);
t_max = max([X(1,:),Y(1,:)]);
t = linspace(t_min-1,t_max+1,100);
p = -a(1)*t/a(2) + b/a(2);

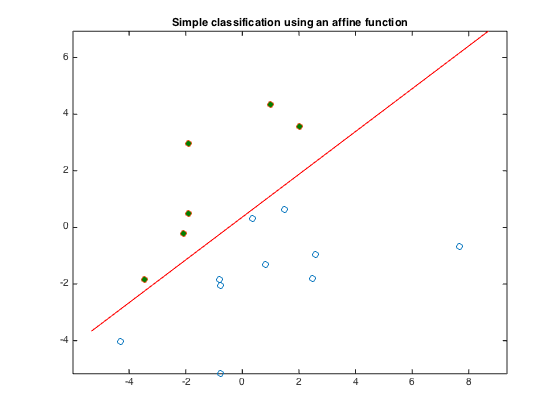
graph = plot(X(1,:),X(2,:), 'o', Y(1,:), Y(2,:), 'o');
set(graph(1),'LineWidth',linewidth);
set(graph(2),'LineWidth',linewidth);
set(graph(2),'MarkerFaceColor',[0 0.5 0]);
hold on;
plot(t,p, '-r');
axis equal
title('Simple classification using an affine function');
% print -deps lin-discr.eps

Finding a separating hyperplane... 
Calling SDPT3 4.0: 16 variables, 3 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints =  3
 dim. of linear var  = 16
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|3.0e+02|1.1e+01|1.9e+03|-1.600000e+02  0.000000e+00| 0:0:00| chol  1  1 
 1|0.677|1.000|9.8e+01|8.0e-02|5.8e+02|-8.715458e+01  0.000000e+00| 0:0:00| chol  1  1 
 2|0.985|1.000|1.5e+00|8.0e-03|8.8e+00|-1.324385e+00  0.000000e+00| 0:0:00| chol  1  1 
 3|0.989|1.000|1.7e-02|8.0e-04|9.8e-02|-1.477477e-02  0.000000e+00| 0:0:00| chol  1  1 
 4|0.989|1.000|1.8e-04|3.4e-03|1.1e-03|-1.625866e-04  0.000000e+00| 0:0:00| chol  1  1 
 5|0.989|1.000|2.0e-06|4.5e-05|1.2e-05|-1.796888e-06  0.000000e+00| 0:0:00| chol  1  1 
 6|0.984|1.000|3.2e-08|4.0e-07|1.9e-07|-2.976878e-08  0.000000e+00| 0:0:00| chol  1  1 
 7|0.987|1.000|4.3e-10|6.5e-09|2.6e-09|-3.939962e-10  0.000000e+00| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   =  7
 primal objective value = -3.93996184e-10
 dual   objective value =  0.00000000e+00
 gap := trace(XZ)       = 2.60e-09
 relative gap           = 2.60e-09
 actual relative gap    = -3.94e-10
 rel. primal infeas (scaled problem)   = 4.33e-10
 rel. dual     "        "       "      = 6.46e-09
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 1.2e-10, 7.0e+00, 6.2e+01
 norm(A), norm(b), norm(C) = 1.7e+01, 1.0e+00, 5.0e+00
 Total CPU time (secs)  = 0.05  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 4.3e-10  0.0e+00  1.6e-08  0.0e+00  -3.9e-10  2.6e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +3.93996e-10
 
Done!