% Section 8.2.1, Boyd & Vandenberghe "Convex Optimization"
% Joelle Skaf - 10/09/05
% (a figure is generated)
%
% Given two polyhedra C = {x | A1*x <= b1} and D = {x | A2*x <= b2}, the
% distance between them is the optimal value of the problem:
%           minimize    || x - y ||_2
%               s.t.    A1*x <= b1
%                       A2*y <= b2
% Note: here x is in R^2

% Input data
randn('seed',0);
n = 2;
m = 2*n;
A1 = randn(m,n);
b1 = randn(m,1);
A2 = randn(m,n);
b2 = randn(m,1);

fprintf(1,'Computing the distance between the 2 polyhedra...');
% Solution via CVX
cvx_begin
    variables x(n) y(n)
    minimize (norm(x - y))
    norm(x,1) <= 2;
    norm(y-[4;3],inf) <=1;
cvx_end

fprintf(1,'Done! \n');

% Displaying results
disp('------------------------------------------------------------------');
disp('The distance between the 2 polyhedra C and D is: ' );
disp(['dist(C,D) = ' num2str(cvx_optval)]);
disp('The optimal points are: ')
disp('x = '); disp(x);
disp('y = '); disp(y);

%Plotting
figure;
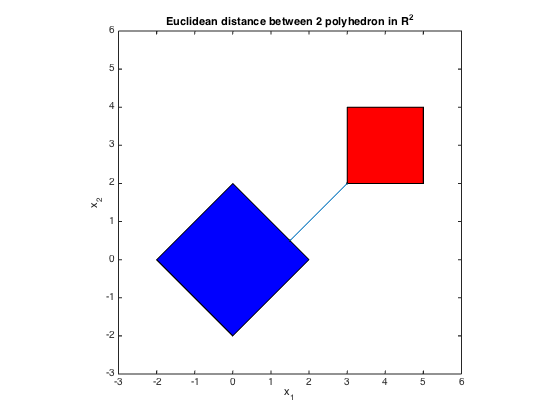
fill([-2; 0; 2; 0],[0;2;0;-2],'b', [3;5;5;3],[2;2;4;4],'r')
axis([-3 6 -3 6])
axis square
hold on;
plot(x(1),x(2),'k.')
plot(y(1),y(2),'k.')
plot([x(1) y(1)],[x(2) y(2)])
title('Euclidean distance between 2 polyhedron in R^2');
xlabel('x_1');
ylabel('x_2');

Computing the distance between the 2 polyhedra... 
Calling SDPT3 4.0: 15 variables, 5 equality constraints
------------------------------------------------------------

 num. of constraints =  5
 dim. of socp   var  = 11,   num. of socp blk  =  5
 dim. of linear var  =  4
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|5.1e+00|1.0e+01|4.4e+02| 3.169873e+00  0.000000e+00| 0:0:00| chol  1  1 
 1|0.634|0.435|1.9e+00|5.9e+00|1.9e+02| 6.002037e+00 -7.087759e+00| 0:0:00| chol  1  1 
 2|0.989|1.000|2.2e-02|1.0e-02|2.8e+01| 6.724918e+00 -1.970669e+01| 0:0:00| chol  1  1 
 3|0.989|0.850|2.3e-04|6.7e-03|4.1e+00| 4.911024e+00  8.498487e-01| 0:0:00| chol  1  1 
 4|0.710|0.705|6.7e-05|2.1e-03|2.1e+00| 3.145473e+00  1.045623e+00| 0:0:00| chol  1  1 
 5|0.979|1.000|1.4e-06|2.3e-05|5.3e-01| 2.358883e+00  1.829442e+00| 0:0:00| chol  1  1 
 6|0.977|0.976|3.2e-08|1.8e-06|1.3e-02| 2.127551e+00  2.114536e+00| 0:0:00| chol  1  1 
 7|0.988|0.986|3.1e-10|1.3e-07|1.6e-04| 2.121394e+00  2.121230e+00| 0:0:00| chol  1  1 
 8|0.987|0.978|4.9e-12|2.9e-09|2.9e-06| 2.121321e+00  2.121318e+00| 0:0:00| chol  1  1 
 9|1.000|0.990|9.7e-14|2.9e-11|1.5e-07| 2.121320e+00  2.121320e+00| 0:0:00| chol  1  1 
10|1.000|0.995|1.6e-16|1.2e-12|3.4e-09| 2.121320e+00  2.121320e+00| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 10
 primal objective value =  2.12132035e+00
 dual   objective value =  2.12132034e+00
 gap := trace(XZ)       = 3.40e-09
 relative gap           = 6.48e-10
 actual relative gap    = 6.47e-10
 rel. primal infeas (scaled problem)   = 1.59e-16
 rel. dual     "        "       "      = 1.16e-12
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 4.2e+00, 1.6e+00, 3.1e+00
 norm(A), norm(b), norm(C) = 4.9e+00, 6.6e+00, 2.0e+00
 Total CPU time (secs)  = 0.13  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 2.1e-16  0.0e+00  1.2e-12  0.0e+00  6.5e-10  6.5e-10
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +2.12132
 
Done! 
------------------------------------------------------------------
The distance between the 2 polyhedra C and D is: 
dist(C,D) = 2.1213
The optimal points are: 
x = 
    1.5000
    0.5000

y = 
    3.0000
    2.0000