% Section 7.1.1
% Boyd & Vandenberghe, "Convex Optimization"
% Kim & Mutapcic, "Logistic regression via geometric programming"
% Written for CVX by Almir Mutapcic 02/08/06
%
% Solves the logistic regression problem re-formulated as a GP.
% The original log regression problem is:
%
%   minimize   sum_i(theta'*x_i) + sum_i( log(1 + exp(-theta'*x_i)) )
%
% where x are explanatory variables and theta are model parameters.
% The equivalent GP is obtained by the following change of variables:
% z_i = exp(theta_i). The log regression problem is then a GP:
%
%   minimize   prod( prod(z_j^x_j) ) * (prod( 1 + prod(z_j^(-x_j)) ))
%
% with variables z and data x (explanatory variables).

randn('state',0);
rand('state',0);

a =  1;
b = -5;

m = 100;
u = 10*rand(m,1);
y = (rand(m,1) < exp(a*u+b)./(1+exp(a*u+b)));

% order the observation data
ind_false = find( y == 0 );
ind_true  = find( y == 1 );

% X is the sorted design matrix
% first have true than false observations followed by the bias term
X = [u(ind_true); u(ind_false)];
X = [X ones(size(u,1),1)];
[m,n] = size(X);
q = length(ind_true);

cvx_begin gp
  % optimization variables
  variables z(n) t(q) s(m)

  minimize( prod(t)*prod(s) )
  subject to
    for k = 1:q
      prod( z.^(X(k,:)') ) <= t(k);
    end

    for k = 1:m
      1 + prod( z.^(-X(k,:)') ) <= s(k);
    end
cvx_end

% retrieve the optimal values and plot the result
theta = log(z);
aml = -theta(1);
bml = -theta(2);

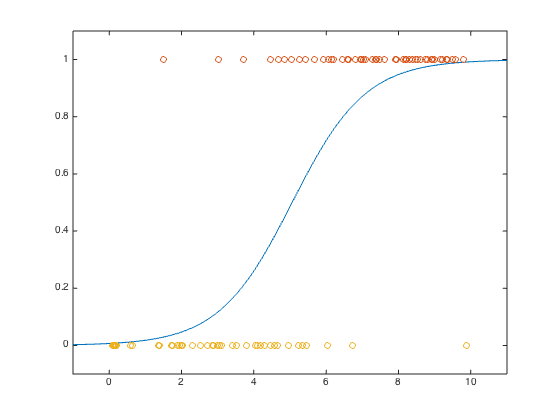
us = linspace(-1,11,1000)';
ps = exp(aml*us + bml)./(1+exp(aml*us+bml));

plot(us,ps,'-', u(ind_true),y(ind_true),'o', ...
                u(ind_false),y(ind_false),'o');
axis([-1, 11,-0.1,1.1]);

 
Successive approximation method to be employed.
   SDPT3 will be called several times to refine the solution.
   Original size: 1320 variables, 401 equality constraints
   200 exponentials add 1600 variables, 1000 equality constraints
-----------------------------------------------------------------
 Cones  |             Errors              |
Mov/Act | Centering  Exp cone   Poly cone | Status
--------+---------------------------------+---------
200/200 | 5.422e+00  2.242e+00  0.000e+00 | Solved
200/200 | 5.049e-01  1.636e-02  0.000e+00 | Solved
194/199 | 2.442e-02  3.881e-05  0.000e+00 | Solved
  0/146 | 3.805e-04  7.816e-09  0.000e+00 | Solved
-----------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +2.10331e+14