% Section 7.1.1
% Boyd & Vandenberghe, "Convex Optimization"
% Original by Lieven Vandenberghe
% Adapted for CVX by Argyris Zymnis - 01/31/06
%
% We consider a binary random variable y with prob(y=1) = p and
% prob(y=0) = 1-p. We assume that that y depends on a vector of
% explanatory variables u in R^n. The logistic model has the form
% p = exp(a'*u+b)/(1+exp(a'*u+b)), where a and b are the model parameters.
% We have m data points (u_1,y_1),...,(u_m,y_m).
% We can reorder the data so that for u_1,..,u_q the outcome is y = 1
% and for u_(q+1),...,u_m the outcome is y = 0. Then it can be shown
% that the ML estimate of a and b can be found by solving
%
% minimize sum_{i=1,..,q}(a'*u_i+b) - sum_i(log(1+exp(a'*u_i+b)))
%
% In this case we have m = 100 and the u_i are just scalars.
% The figure shows the data as well as the function
% f(x) = exp(aml*x+bml)/(1+exp(aml*x+bml)) where aml and bml are the
% ML estimates of a and b.

randn('state',0);
rand('state',0);

% Generate data
a =  1;
b = -5 ;
m= 100;

u = 10*rand(m,1);
y = (rand(m,1) < exp(a*u+b)./(1+exp(a*u+b)));
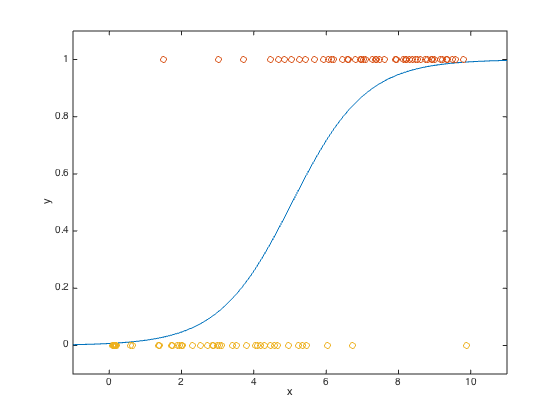
plot(u,y,'o')
axis([-1,11,-0.1, 1.1]);

% Solve problem
%
% minimize  -(sum_(y_i=1) ui)*a - b + sum log (1+exp(a*ui+b)

U = [ones(m,1) u];
cvx_expert true
cvx_begin
    variables x(2)
    maximize(y'*U*x-sum(log_sum_exp([zeros(1,m); x'*U'])))
cvx_end

% Plot results and logistic function

ind1 = find(y==1);
ind2 = find(y==0);

aml = x(2);  bml = x(1);
us = linspace(-1,11,1000)';
ps = exp(aml*us + bml)./(1+exp(aml*us+bml));

dots = plot(us,ps,'-', u(ind1),y(ind1),'o',...
     u(ind2),y(ind2),'o');

axis([-1, 11,-0.1,1.1]);
xlabel('x');
ylabel('y');

 
Successive approximation method to be employed.
   For improved efficiency, SDPT3 is solving the dual problem.
   SDPT3 will be called several times to refine the solution.
   Original size: 600 variables, 202 equality constraints
   200 exponentials add 1600 variables, 1000 equality constraints
-----------------------------------------------------------------
 Cones  |             Errors              |
Mov/Act | Centering  Exp cone   Poly cone | Status
--------+---------------------------------+---------
200/200 | 6.970e+00  2.483e+00  0.000e+00 | Solved
200/200 | 9.608e-01  7.319e-02  0.000e+00 | Solved
199/200 | 1.067e-01  8.487e-04  0.000e+00 | Solved
200/200 | 9.296e-03  6.366e-06  0.000e+00 | Solved
  0/127 | 3.203e-04  6.392e-09  0.000e+00 | Solved
-----------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): -32.9797