Section 7.5.2: Experiment design

Jump to:     Source code     Text output      Plots     Library index

% Boyd & Vandenberghe, "Convex Optimization"
% Original version by Lieven Vandenberghe
% Updated for CVX by Almir Mutapcic - Jan 2006
% (a figure is generated)
%
% This is an example of D-optimal, A-optimal, and E-optimal
% experiment designs.

% problem data
m = 10;
angles1 = linspace(3*pi/4,pi,m);
angles2 = linspace(0,-pi/2,m);

% sensor positions
V = [3.0*[cos(angles1); sin(angles1)], ...
     1.5*[cos(angles2); sin(angles2)]];
p = size(V,2);
n = 2;
noangles = 5000;

% D-optimal design
%
%      maximize    log det V*diag(lambda)*V'
%      subject to  sum(lambda)=1,  lambda >=0
%

% setup the problem and solve it
cvx_begin
  variable lambda(p)
  maximize ( det_rootn( V*diag(lambda)*V' ) )
  subject to
    sum(lambda) == 1;
    lambda >= 0;
cvx_end
lambdaD = lambda; % save the solution for confidence ellipsoids

% plot results
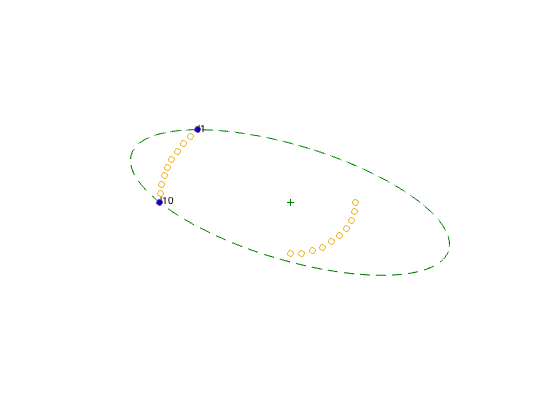
figure(1)
% draw ellipsoid v'*W*v <= 2
W = inv(V*diag(lambda)*V');
angles = linspace(0,2*pi,noangles);
R = chol(W);  % W = R'*R
ellipsoid = sqrt(2)*(R\[cos(angles); sin(angles)]);
d = plot(ellipsoid(1,:), ellipsoid(2,:), '--', 0,0,'+');
set(d, 'Color', [0 0.5 0]); set(d(2),'MarkerFaceColor',[0 0.5 0]);
hold on;

dot=plot(V(1,:),V(2,:),'o');
ind = find(lambda > 0.001);
dots = plot(V(1,ind),V(2,ind),'o');
set(dots,'MarkerFaceColor','blue');

% print out nonzero lambda
disp('Nonzero lambda values for D design:');
for i=1:length(ind)
   text(V(1,ind(i)),V(2,ind(i)), ['l',int2str(ind(i))]);
   disp(['lambda(',int2str(ind(i)),') = ', num2str(lambda(ind(i)))]);
end;

%axis([-4.5 4.5 -4.5 4.5])
axis([-5 5 -5 5])
set(gca,'Xtick',[]);
set(gca,'Ytick',[]);
hold off, axis off
% print -deps Ddesign.eps

% A-optimal design
%
%      minimize    Trace (sum_i lambdai*vi*vi')^{-1}
%      subject to  lambda >= 0, 1'*lambda = 1
%

% SDP formulation
e = eye(2,2);
cvx_begin sdp
  variables lambda(p) u(n)
  minimize ( sum(u) )
  subject to
    for k = 1:n
      [ V*diag(lambda)*V'  e(:,k);
        e(k,:)             u(k)   ] >= 0;
    end
    sum(lambda) == 1;
    lambda >= 0;
cvx_end
lambdaA = lambda; % save the solution for confidence ellipsoids

% plot results
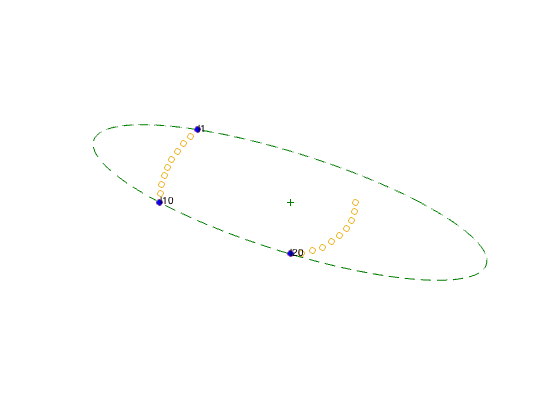
figure(2)
% draw ellipsoid v'*W*v <= mu
W = inv(V*diag(lambda)*V')^2;
mu = diag(V'*W*V);
mu = mean(mu(ind));
angles = linspace(0,2*pi,noangles);
R = chol(W);  % W = R'*R
ellipsoid = sqrt(mu)*(R\[cos(angles); sin(angles)]);
d = plot(ellipsoid(1,:), ellipsoid(2,:), '--',0,0,'+');
set(d, 'Color', [0 0.5 0]);
set(d(2), 'MarkerFaceColor', [0 0.5 0]);
hold on

dot = plot(V(1,:),V(2,:),'o');
ind = find(lambda > 0.001);
dots = plot(V(1,ind),V(2,ind),'o');
set(dots,'MarkerFaceColor','blue');

disp('Nonzero lambda values for A design:');
for i=1:length(ind)
   text(V(1,ind(i)),V(2,ind(i)), ['l',int2str(ind(i))]);
   disp(['lambda(',int2str(ind(i)),') = ', num2str(lambda(ind(i)))]);
end;
%axis([-4.5 4.5 -4.5 4.5])
axis([-5 5 -5 5])
set(gca,'Xtick',[]);
set(gca,'Ytick',[]);
axis off, hold off
% print -deps Adesign.eps

% E-optimal design
%
%      minimize    w
%      subject to  sum_i lambda_i*vi*vi' >= w*I
%                  lambda >= 0,  1'*lambda = 1;
%

cvx_begin sdp
  variables t lambda(p)
  maximize ( t )
  subject to
    V*diag(lambda)*V' >= t*eye(n,n);
    sum(lambda) == 1;
    lambda >= 0;
cvx_end

lambdaE = lambda; % save the solution for confidence ellipsoids

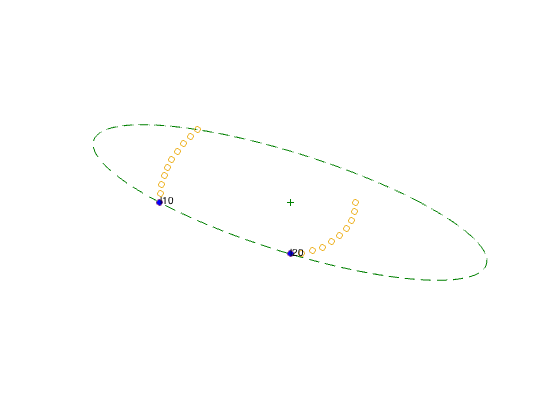
figure(3)
% draw ellipsoid v'*W*v <= mu
mu = diag(V'*W*V);
mu = mean(mu(ind));
angles = linspace(0,2*pi,noangles);
R = chol(W);  % W = R'*R
ellipsoid = sqrt(mu)*(R\[cos(angles); sin(angles)]);
d = plot(ellipsoid(1,:), ellipsoid(2,:), '--', 0, 0, '+');
set(d, 'Color', [0 0.5 0]);
set(d(2), 'MarkerFaceColor', [0 0.5 0]);
hold on

dot = plot(V(1,:),V(2,:),'o');
lambda = lambda(1:p);
ind = find(lambda > 0.001);
dots = plot(V(1,ind),V(2,ind),'o');
set(dots,'MarkerFaceColor','blue');

disp('Nonzero lambda values for E design:');
for i=1:length(ind)
   text(V(1,ind(i)),V(2,ind(i)), ['l',int2str(ind(i))]);
   disp(['lambda(',int2str(ind(i)),') = ', num2str(lambda(ind(i)))]);
end;
%axis([-4.5 4.5 -4.5 4.5])
axis([-5 5 -5 5])
set(gca,'Xtick',[]);
set(gca,'Ytick',[]);
axis off, hold off
% print -deps Edesign.eps


% confidence ellipsoids
eta = 6.2514; % chi2inv(.9,3) value (command available in stat toolbox)
% draw 90 percent confidence ellipsoid  for D design
W = V*diag(lambdaD)*V';
angles = linspace(0,2*pi,noangles);
R = chol(W);  % W = R'*R
ellipsoid = sqrt(eta)*(R\[cos(angles); sin(angles)]);

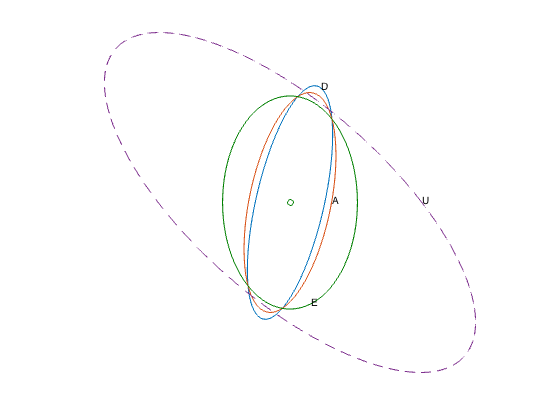
figure(4)
plot(0,0,'ok',ellipsoid(1,:), ellipsoid(2,:), '-');
text(ellipsoid(1,1100),ellipsoid(2,1100),'D');
hold on

% draw 90 percent confidence ellipsoid  for A design
W = V*diag(lambdaA)*V';
angles = linspace(0,2*pi,noangles);
R = chol(W);  % W = R'*R
ellipsoid = sqrt(eta)*(R\[cos(angles); sin(angles)]);
plot(0,0,'ok',ellipsoid(1,:), ellipsoid(2,:), '-');
text(ellipsoid(1,1),ellipsoid(2,1),'A');

% draw 90 percent confidence ellipsoid  for E design
W = V*diag(lambdaE)*V';
angles = linspace(0,2*pi,noangles);
R = chol(W);  % W = R'*R
ellipsoid = sqrt(eta)*(R\[cos(angles); sin(angles)]);
d=plot(0,0,'ok',ellipsoid(1,:), ellipsoid(2,:), '-');
set(d,'Color',[0 0.5 0]);
text(ellipsoid(1,4000),ellipsoid(2,4000),'E');

% draw 90 percent confidence ellipsoid  for uniform design
W_u = inv(V*V'/p);
R = chol(W_u);  % W = R'*R
ellipsoid_u = sqrt(eta)*(R\[cos(angles); sin(angles)]);
plot(ellipsoid_u(1,:), ellipsoid_u(2,:), '--');
text(ellipsoid_u(1),ellipsoid_u(2),'U');
set(gca,'Xtick',[]);
set(gca,'Ytick',[]);
axis off
% print -deps confidence.eps
hold off

 
Calling SDPT3 4.0: 34 variables, 10 equality constraints
------------------------------------------------------------

 num. of constraints = 10
 dim. of sdp    var  =  6,   num. of sdp  blk  =  2
 dim. of linear var  = 21
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|4.8e+02|5.3e+01|5.8e+03| 1.000000e+01  0.000000e+00| 0:0:00| chol  1  1 
 1|0.911|0.847|4.3e+01|8.1e+00|6.0e+02| 8.948551e+00 -2.532080e+01| 0:0:00| chol  1  1 
 2|0.977|1.000|9.7e-01|1.0e-02|5.0e+01| 5.362109e+00 -3.451297e+01| 0:0:00| chol  1  1 
 3|0.987|0.882|1.2e-02|2.1e-03|6.3e+00|-1.337101e+00 -7.637285e+00| 0:0:00| chol  1  1 
 4|0.990|0.859|1.2e-04|2.8e-03|1.3e+00|-2.323773e+00 -3.623790e+00| 0:0:00| chol  1  1 
 5|1.000|1.000|2.6e-08|3.5e-05|5.3e-01|-2.953575e+00 -3.484704e+00| 0:0:00| chol  1  1 
 6|0.978|0.963|4.9e-09|2.3e-06|1.7e-02|-3.172853e+00 -3.190118e+00| 0:0:00| chol  1  1 
 7|0.983|0.985|7.2e-09|1.3e-07|2.7e-04|-3.181834e+00 -3.182106e+00| 0:0:00| chol  1  1 
 8|0.978|0.980|2.3e-08|4.1e-09|5.7e-06|-3.181977e+00 -3.181983e+00| 0:0:00| chol  1  1 
 9|1.000|0.996|2.0e-09|2.2e-09|3.2e-07|-3.181980e+00 -3.181981e+00| 0:0:00| chol  1  1 
10|1.000|1.000|4.6e-11|1.0e-10|1.3e-08|-3.181981e+00 -3.181981e+00| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 10
 primal objective value = -3.18198051e+00
 dual   objective value = -3.18198052e+00
 gap := trace(XZ)       = 1.27e-08
 relative gap           = 1.73e-09
 actual relative gap    = 1.56e-09
 rel. primal infeas (scaled problem)   = 4.63e-11
 rel. dual     "        "       "      = 1.02e-10
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 1.7e+01, 4.3e+00, 7.9e+00
 norm(A), norm(b), norm(C) = 2.9e+01, 2.0e+00, 2.2e+00
 Total CPU time (secs)  = 0.19  
 CPU time per iteration = 0.02  
 termination code       =  0
 DIMACS: 4.6e-11  0.0e+00  1.1e-10  0.0e+00  1.6e-09  1.7e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +3.18198
 
Nonzero lambda values for D design:
lambda(1) = 0.5
lambda(10) = 0.5
 
Calling SDPT3 4.0: 32 variables, 11 equality constraints
------------------------------------------------------------

 num. of constraints = 11
 dim. of sdp    var  =  6,   num. of sdp  blk  =  2
 dim. of linear var  = 20
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|4.9e+02|4.7e+01|5.6e+03| 2.000000e+01  0.000000e+00| 0:0:00| chol  1  1 
 1|0.926|0.999|3.6e+01|1.2e-01|4.2e+02| 1.663772e+01 -2.905847e+01| 0:0:00| chol  1  1 
 2|0.950|1.000|1.8e+00|1.0e-02|4.1e+01| 1.545943e+00 -2.335057e+01| 0:0:00| chol  1  1 
 3|1.000|1.000|3.0e-07|1.0e-03|6.4e+00| 1.636822e+00 -4.755167e+00| 0:0:00| chol  1  1 
 4|0.917|0.879|1.2e-07|2.1e-04|8.7e-01| 1.221243e+00  3.518119e-01| 0:0:00| chol  1  1 
 5|1.000|1.000|2.4e-08|1.0e-05|5.9e-01| 1.101610e+00  5.104357e-01| 0:0:00| chol  1  1 
 6|0.973|0.976|2.4e-09|1.2e-06|9.8e-02| 9.168349e-01  8.188437e-01| 0:0:00| chol  1  1 
 7|1.000|1.000|1.7e-09|1.0e-07|4.1e-02| 8.744063e-01  8.336361e-01| 0:0:00| chol  1  1 
 8|0.971|0.970|8.9e-10|1.3e-08|1.5e-03| 8.505205e-01  8.490159e-01| 0:0:00| chol  1  1 
 9|0.988|0.986|3.2e-10|1.3e-09|1.9e-05| 8.495403e-01  8.495208e-01| 0:0:00| chol  1  1 
10|0.999|0.997|2.4e-13|6.9e-11|3.3e-07| 8.495281e-01  8.495278e-01| 0:0:00| chol  1  1 
11|1.000|1.000|2.4e-11|1.0e-12|1.1e-08| 8.495279e-01  8.495279e-01| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 11
 primal objective value =  8.49527931e-01
 dual   objective value =  8.49527921e-01
 gap := trace(XZ)       = 1.08e-08
 relative gap           = 3.99e-09
 actual relative gap    = 3.98e-09
 rel. primal infeas (scaled problem)   = 2.36e-11
 rel. dual     "        "       "      = 1.00e-12
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 8.1e+00, 1.7e+00, 2.8e+00
 norm(A), norm(b), norm(C) = 4.0e+01, 2.7e+00, 2.4e+00
 Total CPU time (secs)  = 0.19  
 CPU time per iteration = 0.02  
 termination code       =  0
 DIMACS: 3.2e-11  0.0e+00  1.2e-12  0.0e+00  4.0e-09  4.0e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.849528
 
Nonzero lambda values for A design:
lambda(1) = 0.2966
lambda(10) = 0.37797
lambda(20) = 0.32543
 
Calling SDPT3 4.0: 23 variables, 3 equality constraints
------------------------------------------------------------

 num. of constraints =  3
 dim. of sdp    var  =  2,   num. of sdp  blk  =  1
 dim. of linear var  = 20
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|3.4e+02|5.3e+00|5.2e+03|-8.321762e+02  0.000000e+00| 0:0:00| chol  1  1 
 1|0.987|0.998|4.4e+00|3.1e-02|9.8e+01|-3.661832e+00 -2.519810e+01| 0:0:00| chol  1  1 
 2|1.000|1.000|7.7e-07|1.9e-03|1.3e+01|-5.769039e-01 -1.375481e+01| 0:0:00| chol  1  1 
 3|1.000|0.900|1.8e-07|3.6e-04|1.3e+00|-7.288098e-01 -2.061763e+00| 0:0:00| chol  1  1 
 4|0.763|1.000|3.2e-08|1.9e-05|9.0e-01|-1.574210e+00 -2.470832e+00| 0:0:00| chol  1  1 
 5|1.000|0.948|1.3e-09|2.8e-06|6.7e-02|-1.752692e+00 -1.819600e+00| 0:0:00| chol  1  1 
 6|0.982|0.984|2.5e-10|2.3e-07|1.2e-03|-1.799172e+00 -1.800349e+00| 0:0:00| chol  1  1 
 7|0.989|0.989|8.5e-11|2.1e-08|1.3e-05|-1.799991e+00 -1.800004e+00| 0:0:00| chol  1  1 
 8|0.993|0.991|2.8e-09|2.1e-10|2.4e-07|-1.800000e+00 -1.800000e+00| 0:0:00| chol  1  1 
 9|0.995|0.992|1.3e-09|2.7e-11|4.0e-09|-1.800000e+00 -1.800000e+00| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   =  9
 primal objective value = -1.79999999e+00
 dual   objective value = -1.80000000e+00
 gap := trace(XZ)       = 3.99e-09
 relative gap           = 8.67e-10
 actual relative gap    = 1.23e-09
 rel. primal infeas (scaled problem)   = 1.27e-09
 rel. dual     "        "       "      = 2.70e-11
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 8.2e-01, 2.1e+00, 5.9e+00
 norm(A), norm(b), norm(C) = 2.5e+01, 2.0e+00, 2.5e+01
 Total CPU time (secs)  = 0.13  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 1.3e-09  0.0e+00  6.7e-11  0.0e+00  1.2e-09  8.7e-10
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +1.8
 
Nonzero lambda values for E design:
lambda(10) = 0.2
lambda(20) = 0.8