Example 6.8: Spline fitting

Jump to:     Source code     Text output      Plots     Library index

% Section 6.5.3, Figure 6.20
% Boyd & Vandenberghe "Convex Optimization"
% Original by Lieven Vandenberghe
% Adapted for CVX by Joelle Skaf - 10/03/05
% (a figure is generated)
%
% Given data u_1,...,u_m and v_1,...,v_m in R, the goal is to fit to the
% data piecewise polynomials with maximum degree 3 (with continuous first
% and second derivatives).
% The [0,1] interval is divided into 3 equal intervals: [-1, -1/3],
% [-1/3,1/3], [1/3,1] with the following polynomials defined on each
% interval respectively:
% p1(t) = x11 + x12*t + x13*t^2 + x14*t^3
% p2(t) = x21 + x22*t + x23*t^2 + x24*t^3
% p3(t) = x31 + x32*t + x33*t^2 + x34*t^3
% L2-norm and Linfty-norm cases are considered

% Input Data
n=4;  % variables per segment
m=40;
randn('state',0);
% generate 50 points ui, vi
u = linspace(-1,1,m);
v = 1./(5+40*u.^2) + 0.1*u.^3 + 0.01*randn(1,m);

a = -1/3;  b = 1/3;  % boundary points
u1 = u(find(u<a)); m1 = length(u1);
u2 = u(find((u >= a) & (u<b)));  m2 = length(u2);
u3 = u(find((u >= b)));  m3 = length(u3);

A1 = vander(u1');   A1 = fliplr(A1(:,m1-n+[1:n]));
A2 = vander(u2');   A2 = fliplr(A2(:,m2-n+[1:n]));
A3 = vander(u3');   A3 = fliplr(A3(:,m3-n+[1:n]));

%L-2 fit
fprintf(1,'Computing splines in the case of L2-norm...');

cvx_begin
    variables x1(n) x2(n) x3(n)
    minimize ( norm( [A1*x1;A2*x2;A3*x3] - v') )
    %continuity conditions at point a
    [1 a a^2   a^3]*x1 == [1 a a^2   a^3]*x2;
    [0 1 2*a 3*a^2]*x1 == [0 1 2*a 3*a^2]*x2;
    [0 0   2 6*a  ]*x1 == [0 0   2 6*a  ]*x2;
    %continuity conditions at point b
    [1 b b^2   b^3]*x2 == [1 b b^2   b^3]*x3;
    [0 1 2*b 3*b^2]*x2 == [0 1 2*b 3*b^2]*x3;
    [0 0   2 6*b  ]*x2 == [0 0   2 6*b  ]*x3;
cvx_end

fprintf(1,'Done! \n');

% L-infty fit
fprintf(1,'Computing splines in the case of Linfty-norm...');

cvx_begin
    variables xl1(n) xl2(n) xl3(n)
    minimize ( norm( [A1*xl1;A2*xl2;A3*xl3] - v', inf) )
    %continuity conditions at point a
    [1 a a^2   a^3]*xl1 == [1 a a^2   a^3]*xl2;
    [0 1 2*a 3*a^2]*xl1 == [0 1 2*a 3*a^2]*xl2;
    [0 0   2 6*a  ]*xl1 == [0 0   2 6*a  ]*xl2;
    %continuity conditions at point b
    [1 b b^2   b^3]*xl2 == [1 b b^2   b^3]*xl3;
    [0 1 2*b 3*b^2]*xl2 == [0 1 2*b 3*b^2]*xl3;
    [0 0   2 6*b  ]*xl2 == [0 0   2 6*b  ]*xl3;
cvx_end

fprintf(1,'Done! \n');

% evaluate the interpolating polynomials using Horner's method
u1s = linspace(-1.0,a,1000)';
p1 = x1(1) + x1(2)*u1s + x1(3)*u1s.^2 + x1(4).*u1s.^3;
p1l1 = xl1(1) + xl1(2)*u1s + xl1(3)*u1s.^2 + xl1(4).*u1s.^3;

u2s = linspace(a,b,1000)';
p2 = x2(1) + x2(2)*u2s + x2(3)*u2s.^2 + x2(4).*u2s.^3;
p2l1 = xl2(1) + xl2(2)*u2s + xl2(3)*u2s.^2 + xl2(4).*u2s.^3;

u3s = linspace(b,1.0,1000)';
p3 = x3(1) + x3(2)*u3s + x3(3)*u3s.^2 + x3(4).*u3s.^3;
p3l1 = xl3(1) + xl3(2)*u3s + xl3(3)*u3s.^2 + xl3(4).*u3s.^3;

us = [u1s;u2s;u3s];
p = [p1;p2;p3];
pl = [p1l1;p2l1;p3l1];
% plot function and cubic splines
d = plot(us,p,'b-',u,v,'go', us,pl,'r--',...
         [-1 -1], [-0.1 0.25], 'k--', [1 1], [-0.1 0.25], 'k--', ...
         [a a], [-0.1 0.25], 'k--', [b b], [-0.1 0.25], 'k--');

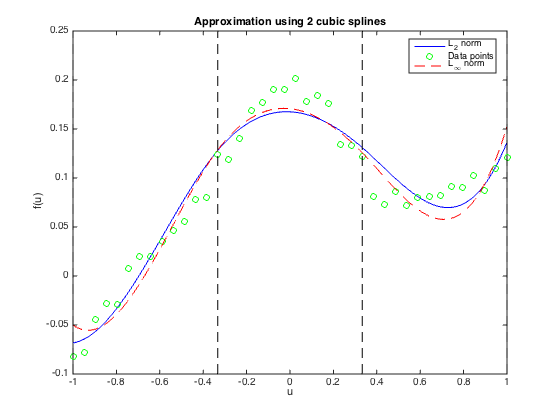
title('Approximation using 2 cubic splines');
xlabel('u');
ylabel('f(u)');
legend('L_2 norm','Data points','L_{\infty} norm', 'Location','Best');
% print -deps splineapprox.eps

Computing splines in the case of L2-norm... 
Calling SDPT3 4.0: 47 variables, 13 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 13
 dim. of socp   var  = 41,   num. of socp blk  =  1
 dim. of free   var  =  6 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|2.7e+00|3.7e+01|5.3e+03| 0.000000e+00  0.000000e+00| 0:0:00| chol  1  1 
 1|1.000|0.992|5.5e-06|4.0e-01|1.6e+01|-5.556583e-03 -4.475983e+00| 0:0:00| chol  1  1 
 2|1.000|0.964|5.9e-07|2.4e-02|2.9e-01|-1.143822e-02 -1.665989e-01| 0:0:00| chol  1  1 
 3|0.940|0.914|2.5e-07|3.0e-03|1.6e-02|-1.120732e-01 -1.224254e-01| 0:0:00| chol  1  1 
 4|0.986|0.986|1.3e-07|1.4e-04|2.1e-04|-1.165416e-01 -1.165974e-01| 0:0:00| chol  1  1 
 5|0.989|0.988|7.2e-09|8.8e-06|4.1e-06|-1.166027e-01 -1.165942e-01| 0:0:00| chol  1  1 
 6|0.992|0.985|1.8e-09|1.4e-07|6.4e-08|-1.166034e-01 -1.166032e-01| 0:0:00| chol  1  1 
 7|1.000|0.961|1.3e-11|4.7e-09|1.4e-09|-1.166034e-01 -1.166034e-01| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   =  7
 primal objective value = -1.16603357e-01
 dual   objective value = -1.16603352e-01
 gap := trace(XZ)       = 1.38e-09
 relative gap           = 1.12e-09
 actual relative gap    = -4.42e-09
 rel. primal infeas (scaled problem)   = 1.27e-11
 rel. dual     "        "       "      = 4.74e-09
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 1.5e+00, 1.9e+00, 1.6e-01
 norm(A), norm(b), norm(C) = 1.3e+01, 2.0e+00, 1.7e+00
 Total CPU time (secs)  = 0.10  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 1.3e-11  0.0e+00  6.8e-09  0.0e+00  -4.4e-09  1.1e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.116603
 
Done! 
Computing splines in the case of Linfty-norm... 
Calling SDPT3 4.0: 126 variables, 53 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 53
 dim. of socp   var  = 80,   num. of socp blk  = 40
 dim. of linear var  = 40
 dim. of free   var  =  6 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|4.5e+01|5.9e+01|1.1e+04| 0.000000e+00  0.000000e+00| 0:0:00| chol  1  1 
 1|0.991|0.990|4.0e-01|6.8e-01|7.7e+01|-2.313753e-04 -1.682246e+01| 0:0:00| chol  1  1 
 2|1.000|0.999|2.3e-05|1.1e-02|7.5e+00|-2.255710e-04 -7.490910e+00| 0:0:00| chol  1  1 
 3|1.000|0.945|5.7e-05|1.5e-03|4.2e-01|-1.036680e-03 -4.179648e-01| 0:0:00| chol  1  1 
 4|0.997|0.887|3.1e-06|2.7e-04|1.4e-01|-1.142045e-02 -1.515088e-01| 0:0:00| chol  1  1 
 5|1.000|0.685|1.4e-05|9.2e-05|4.6e-02|-1.557158e-02 -6.132604e-02| 0:0:00| chol  1  1 
 6|1.000|0.092|5.1e-06|8.5e-05|3.8e-02|-2.134726e-02 -5.863361e-02| 0:0:00| chol  2  2 
 7|1.000|0.427|4.6e-06|5.0e-05|2.2e-02|-2.518940e-02 -4.699203e-02| 0:0:00| chol  2  2 
 8|1.000|0.467|1.9e-06|2.7e-05|1.1e-02|-2.900580e-02 -3.963163e-02| 0:0:00| chol  2  1 
 9|1.000|0.549|5.4e-07|8.3e-05|4.5e-03|-3.107602e-02 -3.531163e-02| 0:0:00| chol  1  1 
10|1.000|0.931|9.1e-09|3.5e-05|3.9e-04|-3.187530e-02 -3.223669e-02| 0:0:00| chol  1  1 
11|0.984|0.984|1.9e-10|3.0e-06|6.8e-06|-3.203558e-02 -3.204147e-02| 0:0:00| chol  1  1 
12|0.992|0.989|3.5e-12|5.2e-08|1.2e-07|-3.203827e-02 -3.203838e-02| 0:0:00| chol  1  1 
13|0.993|0.989|1.7e-12|8.9e-10|1.8e-09|-3.203833e-02 -3.203834e-02| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 13
 primal objective value = -3.20383334e-02
 dual   objective value = -3.20383351e-02
 gap := trace(XZ)       = 1.81e-09
 relative gap           = 1.70e-09
 actual relative gap    = 1.56e-09
 rel. primal infeas (scaled problem)   = 1.72e-12
 rel. dual     "        "       "      = 8.88e-10
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 8.2e-01, 2.4e+00, 2.1e-01
 norm(A), norm(b), norm(C) = 1.8e+01, 2.0e+00, 1.7e+00
 Total CPU time (secs)  = 0.18  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 1.7e-12  0.0e+00  1.3e-09  0.0e+00  1.6e-09  1.7e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.0320383
 
Done!