% Boyd & Vandenberghe "Convex Optimization"
% Almir Mutapcic - 01/30/06
% Updated to use GP mode 02/08/06
% (a figure is generated)
%
% We have a segmented cantilever beam with N segments. Each segment
% has a unit length and variable width and height (rectangular profile).
% The goal is minimize the total volume of the beam, over all segment
% widths w_i and heights h_i, subject to constraints on aspect ratios,
% maximum allowable stress in the material, vertical deflection y, etc.
%
% The problem can be posed as a geometric program (posynomial form)
%     minimize    sum( w_i* h_i)
%         s.t.    w_min <= w_i <= w_max,       for all i = 1,...,N
%                 h_min <= h_i <= h_max
%                 S_min <= h_i/w_i <= S_max
%                 6*i*F/(w_i*h_i^2) <= sigma_max
%                 6*F/(E*w_i*h_i^3) == d_i
%                 (2*i - 1)*d_i + v_(i+1) <= v_i
%                 (i - 1/3)*d_i + v_(i+1) + y_(i+1) <= y_i
%                 y_1 <= y_max
%
% with variables w_i, h_i, d_i, (i = 1,...,N) and v_i, y_i (i = 1,...,N+1).
% (Consult the book for other definitions and a recursive formulation of
% this problem.)

% optimization variables
N = 8;

% constants
wmin = .1; wmax = 100;
hmin = .1; hmax = 6;
Smin = 1/5; Smax = 5;
sigma_max = 1;
ymax = 10;
E = 1; F = 1;

cvx_begin gp
  % optimization variables
  variables w(N) h(N) v(N+1) y(N+1);

  % objective is the total volume of the beam
  % obj = sum of (widths*heights*lengths) over each section
  % (recall that the length of each segment is set to be 1)
  minimize( w'*h )
  subject to
    % non-recursive formulation
    d = 6*F*ones(N,1)./(E*ones(N,1).*w.*h.^3);
    for i = 1:N
      (2*i-1)*d(i) + v(i+1) <= v(i);
      (i-1/3)*d(i) + v(i+1) + y(i+1) <= y(i);
    end

    % constraint set
    wmin <= w    <= wmax;
    hmin <= h    <= hmax;
    Smin <= h./w <= Smax;
    6*F*[1:N]'./(w.*(h.^2)) <= sigma_max;
    y(1) <= ymax;
cvx_end

% display results
disp('The optimal widths and heights are: ');
w, h
fprintf(1,'The optimal minimum volume of the beam is %3.4f.\n', sum(w.*h))

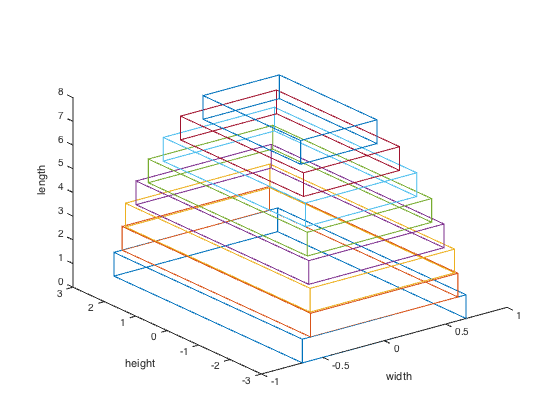
% plot the 3D model of the optimal cantilever beam
figure, clf
cantilever_beam_plot([h; w])

 
Successive approximation method to be employed.
   SDPT3 will be called several times to refine the solution.
   Original size: 323 variables, 144 equality constraints
   48 exponentials add 384 variables, 240 equality constraints
-----------------------------------------------------------------
 Cones  |             Errors              |
Mov/Act | Centering  Exp cone   Poly cone | Status
--------+---------------------------------+---------
 26/ 26 | 8.000e+00  7.849e-01  0.000e+00 | Solved
 42/ 43 | 3.803e-01  9.215e-03  0.000e+00 | Solved
 34/ 40 | 1.422e-02  1.389e-05  0.000e+00 | Solved
  6/ 10 | 1.760e-03  1.263e-07  0.000e+00 | Solved
  0/  0 | 1.747e-04  0.000e+00  0.000e+00 | Solved
-----------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +42.3965
 
The optimal widths and heights are: 

w =

    0.6214
    0.7830
    0.9060
    1.0124
    1.1004
    1.1762
    1.2000
    1.3333


h =

    3.1072
    3.9149
    4.5298
    5.0620
    5.5019
    5.8811
    6.0000
    6.0000

The optimal minimum volume of the beam is 42.3965.