% "FIR Filter Design via Spectral Factorization and Convex Optimization" example
% by S.-P. Wu, S. Boyd, and L. Vandenberghe
% (figures are generated)
%
% Designs a uniform linear antenna array using spectral factorization method where:
% - it minimizes sidelobe level outside the beamwidth of the pattern
% - it has a constraint on the maximum ripple around unit gain in the beamwidth
%
%   minimize   max |y(theta)|                   for theta in the stop-beamwidth
%       s.t.   1/delta <= |y(theta)| <= delta   for theta in the pass-beamwidth
%
% We first replace the look-angle variable theta with the "frequency"
% variable omega, defined by omega = -2*pi*d/lambda*cos(theta).
% This transforms the antenna pattern y(theta) into a standard discrete
% Fourier transform of array weights w. Then we apply another change of
% variables: we replace w with its auto-correlation coefficients r.
%
% Now the problem can be solved via spectral factorization approach:
%
%   minimize   max R(omega)                        for omega in the stopband
%       s.t.   (1/delta)^2 <= R(omega) <= delta^2  for omega in the passband
%              R(omega) >= 0                       for all omega
%
% where R(omega) is the squared magnitude of the y(theta) array response
% (and the Fourier transform of the autocorrelation coefficients r).
% Variables are coefficients r. delta is the allowed passband ripple.
% This is a convex problem (can be formulated as an LP after sampling).
%
% Written for CVX by Almir Mutapcic 02/02/06

%********************************************************************
% problem specs: a uniform line array with inter-element spacing d
%                antenna element locations are at d*[0:n-1]
%                (the array pattern will be symmetric around origin)
%********************************************************************
n = 20;               % number of antenna elements
lambda = 1;           % wavelength
d = 0.45*lambda;      % inter-element spacing

% passband direction from 30 to 60 degrees (30 degrees bandwidth)
% transition band is 15 degrees on both sides of the passband
theta_pass = 40;
theta_stop = 50;

% passband max allowed ripple
ripple = 0.1; % in dB (+/- around the unit gain)

%********************************************************************
% construct optimization data
%********************************************************************
% number of frequency samples
m = 30*n;

% convert passband and stopband angles into omega frequencies
omega_zero = -2*pi*d/lambda;
omega_pass = -2*pi*d/lambda*cos(theta_pass*pi/180);
omega_stop = -2*pi*d/lambda*cos(theta_stop*pi/180);
omega_pi   = +2*pi*d/lambda;

% build matrix A that relates R(omega) and r, ie, R = A*r
omega = linspace(-pi,pi,m)';
A = exp( -j*omega(:)*[1-n:n-1] );

% passband constraint matrix
Ap = A(omega >= omega_zero & omega <= omega_pass,:);

% stopband constraint matrix
As = A(omega >= omega_stop & omega <= omega_pi,:);

%********************************************************************
% formulate and solve the magnitude design problem
%********************************************************************
cvx_begin
  variable r(2*n-1,1) complex
  % minimize stopband attenuation
  minimize( max( real( As*r ) ) )
  subject to
    % passband ripple constraints
    (10^(-ripple/20))^2 <= real( Ap*r ) <= (10^(+ripple/20))^2;
    % nonnegative-real constraint for all frequencies
    % a bit redundant: the passband frequencies are already constrained
    real( A*r ) >= 0;
    % auto-correlation symmetry constraints
    imag(r(n)) == 0;
    r(n-1:-1:1) == conj(r(n+1:end));
cvx_end

% check if problem was successfully solved
if ~strfind(cvx_status,'Solved')
    return
end

% find antenna weights by computing the spectral factorization
w = spectral_fact(r);

% divided by 2 since this is in PSD domain
min_sidelobe_level = 10*log10( cvx_optval );
fprintf(1,'The minimum sidelobe level is %3.2f dB.\n\n',...
          min_sidelobe_level);

%********************************************************************
% plots
%********************************************************************
% build matrix G that relates y(theta) and w, ie, y = G*w
theta = [-180:180]';
G = kron( cos(pi*theta/180), [0:n-1] );
G = exp(2*pi*i*d/lambda*G);
y = G*w;

% plot array pattern
figure(1), clf
ymin = -40; ymax = 5;
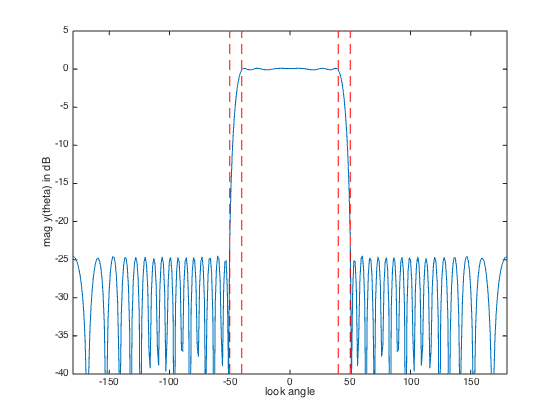
plot([-180:180], 20*log10(abs(y)), ...
     [theta_stop theta_stop],[ymin ymax],'r--',...
     [-theta_pass -theta_pass],[ymin ymax],'r--',...
     [-theta_stop -theta_stop],[ymin ymax],'r--',...
     [theta_pass theta_pass],[ymin ymax],'r--');
xlabel('look angle'), ylabel('mag y(theta) in dB');
axis([-180 180 ymin ymax]);

% polar plot
figure(2), clf
zerodB = 50;
dBY = 20*log10(abs(y)) + zerodB;
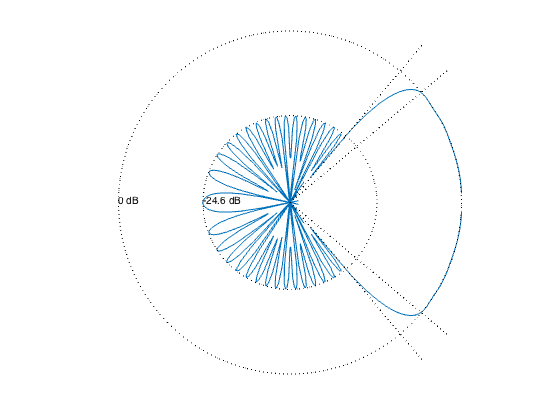
plot(dBY.*cos(pi*theta/180), dBY.*sin(pi*theta/180), '-');
axis([-zerodB zerodB -zerodB zerodB]), axis('off'), axis('square')
hold on
plot(zerodB*cos(pi*theta/180),zerodB*sin(pi*theta/180),'k:') % 0 dB
plot( (min_sidelobe_level + zerodB)*cos(pi*theta/180), ...
      (min_sidelobe_level + zerodB)*sin(pi*theta/180),'k:')  % min level
text(-zerodB,0,'0 dB')
text(-(min_sidelobe_level + zerodB),0,sprintf('%0.1f dB',min_sidelobe_level));
plot([0 60*cos(theta_pass*pi/180)], [0 60*sin(theta_pass*pi/180)], 'k:')
plot([0 60*cos(-theta_pass*pi/180)],[0 60*sin(-theta_pass*pi/180)],'k:')
plot([0 60*cos(theta_stop*pi/180)], [0 60*sin(theta_stop*pi/180)], 'k:')
plot([0 60*cos(-theta_stop*pi/180)],[0 60*sin(-theta_stop*pi/180)],'k:')
hold off

 
Calling SDPT3 4.0: 1171 variables, 40 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 40
 dim. of linear var  = 1171
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|1.0e+04|1.4e+02|2.0e+06| 1.008655e+02  0.000000e+00| 0:0:00| chol  1  1 
 1|0.875|0.762|1.3e+03|3.4e+01|3.1e+05| 1.707706e+03 -8.318726e+01| 0:0:00| chol  1  1 
 2|0.763|0.812|3.0e+02|6.5e+00|8.5e+04| 2.032831e+03 -1.284834e+02| 0:0:00| chol  1  1 
 3|0.879|0.798|3.6e+01|1.3e+00|1.4e+04| 1.364175e+03 -1.494646e+02| 0:0:00| chol  1  1 
 4|0.662|0.834|1.2e+01|2.3e-01|5.5e+03| 8.085569e+02 -2.002852e+02| 0:0:00| chol  1  1 
 5|0.934|1.000|8.1e-01|2.4e-03|6.0e+02| 1.565080e+02 -1.927015e+02| 0:0:00| chol  2  2 
 6|0.903|0.981|7.9e-02|2.8e-04|1.1e+02| 2.233473e+01 -7.632890e+01| 0:0:00| chol  2  2 
 7|0.862|1.000|1.1e-02|1.6e-02|6.9e+01| 1.487219e+01 -5.065246e+01| 0:0:00| chol  1  1 
 8|0.930|0.941|7.7e-04|3.1e-03|4.5e+00| 1.679599e+00 -2.798362e+00| 0:0:00| chol  1  1 
 9|0.473|0.949|4.0e-04|3.1e-04|2.4e+00| 9.986219e-01 -1.431647e+00| 0:0:00| chol  1  1 
10|0.872|1.000|5.2e-05|8.1e-05|1.2e+00| 2.761667e-01 -8.786424e-01| 0:0:00| chol  1  1 
11|0.951|0.988|2.5e-06|1.1e-05|1.9e-01| 6.218113e-02 -1.316351e-01| 0:0:00| chol  1  1 
12|0.662|1.000|8.5e-07|5.0e-07|8.7e-02| 2.910117e-02 -5.759656e-02| 0:0:00| chol  1  1 
13|0.847|0.705|1.3e-07|3.2e-07|4.4e-02| 8.825548e-03 -3.492830e-02| 0:0:00| chol  1  1 
14|1.000|0.570|5.6e-14|1.6e-07|2.9e-02| 4.098110e-03 -2.443245e-02| 0:0:00| chol  1  1 
15|1.000|1.000|4.2e-14|1.2e-12|1.4e-02| 2.591040e-03 -1.164488e-02| 0:0:00| chol  1  1 
16|1.000|0.990|3.6e-14|1.0e-12|6.3e-03| 3.772454e-04 -5.904202e-03| 0:0:00| chol  1  1 
17|0.404|1.000|7.4e-14|1.0e-12|4.7e-03|-4.331405e-04 -5.174142e-03| 0:0:00| chol  1  1 
18|0.807|1.000|9.9e-14|1.0e-12|2.4e-03|-1.819613e-03 -4.250844e-03| 0:0:00| chol  1  1 
19|0.980|0.981|6.3e-13|1.0e-12|7.3e-04|-2.854651e-03 -3.581003e-03| 0:0:00| chol  1  1 
20|0.572|0.971|3.7e-12|1.0e-12|3.6e-04|-3.103962e-03 -3.459133e-03| 0:0:00| chol  1  1 
21|0.827|0.950|7.7e-13|1.1e-12|9.7e-05|-3.339091e-03 -3.436323e-03| 0:0:00| chol  1  1 
22|0.970|0.894|6.4e-12|1.1e-12|9.6e-06|-3.419536e-03 -3.429101e-03| 0:0:00| chol  1  1 
23|0.866|0.886|2.5e-12|1.4e-12|1.8e-06|-3.426509e-03 -3.428273e-03| 0:0:00| chol  1  1 
24|0.979|0.983|1.5e-12|1.0e-12|8.9e-08|-3.428062e-03 -3.428151e-03| 0:0:00| chol  1  1 
25|0.992|0.993|1.3e-12|1.0e-12|1.8e-09|-3.428145e-03 -3.428147e-03| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 25
 primal objective value = -3.42814510e-03
 dual   objective value = -3.42814686e-03
 gap := trace(XZ)       = 1.76e-09
 relative gap           = 1.74e-09
 actual relative gap    = 1.74e-09
 rel. primal infeas (scaled problem)   = 1.30e-12
 rel. dual     "        "       "      = 1.01e-12
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 7.2e-01, 2.9e-01, 9.2e+00
 norm(A), norm(b), norm(C) = 3.0e+02, 2.0e+00, 1.2e+01
 Total CPU time (secs)  = 0.31  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 1.3e-12  0.0e+00  6.1e-12  0.0e+00  1.7e-09  1.7e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.00342815
 
The minimum sidelobe level is -24.65 dB.