The Water Tank
Solution

To do this problem, we have a couple of useful tools. First, it's easy to measure the area of a circular sector, that is, the region between any two lines from the center of the circle. If we measure the angle A between these lines in radians, then

sector_area = 1/2 * R**2 * A

Now let's suppose that the water height H is less than the radius R of the circle. Then, if we can determine where the water surface contacts the two sides of the circle, the wet area is entirely contained in the circular sector between those two contact points. In fact, the circular sector can be divided into two regions, the wet area, and a triangular dry area. Now our task can be written as:

wet_area = sector_area - triangle_area

Now draw a vertical line from the center downwards. It will cross the water surface and continue to the circle's edge. This forms a right triangle, with a central angle equal to A/2. Now the adjacent side of the right triangle has length R-H, and the hypotenuse is R, so the opposite side must have length sqrt ( H * ( 2 * R - H ) ). This right triangle is half of the dry triangular area. We have just determined its two sides, so its area is half the product of the two sides, and the total area is twice that:

triangle_area = ( R - H ) * sqrt ( H * ( 2 * R - H ) )

All that remains is to determine the total sector area. For that, we need the angle A. But from our right triangle, we know something about the angle A/2, that is, its tangent:

tan ( A/2 ) = sqrt ( H * ( 2 * R - H ) ) / ( R - H )

cos ( A/2 ) = ( R - H ) / R

A = 2 * arccos ( ( R - H ) / R )

This gives us the formula

wet_area = sector_area - triangle_area
= 0.5 * R**2 * 2 * arccos ( ( R - H ) / R ) - ( R - H ) * sqrt ( H * ( 2 * R - H ) )

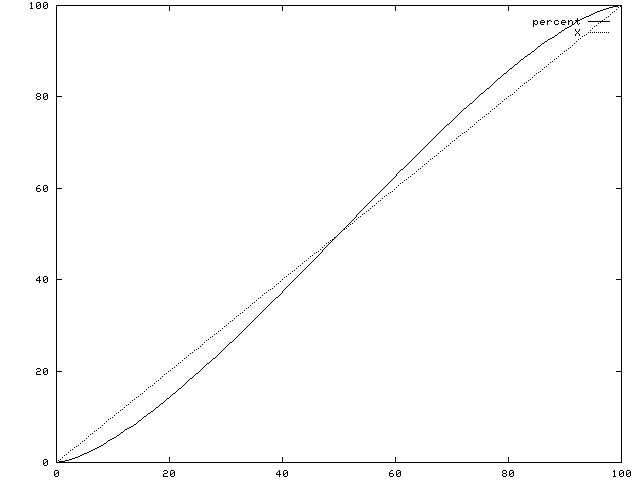
Here is a graph in which the horizontal axis is the water height, as a percentage of the diameter, and the vertical axis is the percentage of the total area that is under water. We also plot a diagonal line ( which would represent a square tank) for comparison.

Here is a table of the results for a circle of radius 50:

Water Height	Wet Area	Percent Wet
0	0.00	0.00
1	13.29	0.17
2	37.49	0.48
3	68.66	0.87
4	105.38	1.34
5	146.81	1.87
6	192.39	2.45
7	241.68	3.08
8	294.35	3.75
9	350.12	4.46
10	408.75	5.20
11	470.06	5.98
12	533.85	6.80
13	599.99	7.64
14	668.33	8.51
15	738.75	9.41
16	811.12	10.33
17	885.36	11.27
18	961.35	12.24
19	1039.00	13.23
20	1118.24	14.24
21	1198.98	15.27
22	1281.14	16.31
23	1364.65	17.38
24	1449.45	18.45
25	1535.46	19.55
26	1622.63	20.66
27	1710.90	21.78
28	1800.20	22.92
29	1890.48	24.07
30	1981.68	25.23
31	2073.76	26.40
32	2166.66	27.59
33	2260.34	28.78
34	2354.73	29.98
35	2449.80	31.19
36	2545.51	32.41
37	2641.79	33.64
38	2738.61	34.87
39	2835.93	36.11
40	2933.70	37.35
41	3031.87	38.60
42	3130.42	39.86
43	3229.28	41.12
44	3328.43	42.38
45	3427.83	43.64
46	3527.42	44.91
47	3627.17	46.18
48	3727.04	47.45
49	3827.00	48.73
50	3926.99	50.00
51	4026.98	51.27
52	4126.94	52.55
53	4226.81	53.82
54	4326.56	55.09
55	4426.16	56.36
56	4525.55	57.62
57	4624.70	58.88
58	4723.56	60.14
59	4822.11	61.40
60	4920.28	62.65
61	5018.05	63.89
62	5115.37	65.13
63	5212.19	66.36
64	5308.48	67.59
65	5404.18	68.81
66	5499.25	70.02
67	5593.64	71.22
68	5687.32	72.41
69	5780.22	73.60
70	5872.30	74.77
71	5963.50	75.93
72	6053.79	77.08
73	6143.09	78.22
74	6231.35	79.34
75	6318.52	80.45
76	6404.53	81.55
77	6489.33	82.62
78	6572.84	83.69
79	6655.01	84.73
80	6735.74	85.76
81	6814.98	86.77
82	6892.64	87.76
83	6968.63	88.73
84	7042.86	89.67
85	7115.23	90.59
86	7185.65	91.49
87	7253.99	92.36
88	7320.13	93.20
89	7383.93	94.02
90	7445.23	94.80
91	7503.86	95.54
92	7559.63	96.25
93	7612.30	96.92
94	7661.59	97.55
95	7707.17	98.13
96	7748.60	98.66
97	7785.33	99.13
98	7816.50	99.52
99	7840.69	99.83
100	7853.98	100.00

Back to the The Watertank Puzzle.