Let us first note that little Debbie is exactly 1/1000 of a mile tall, a quantity which we will call T.
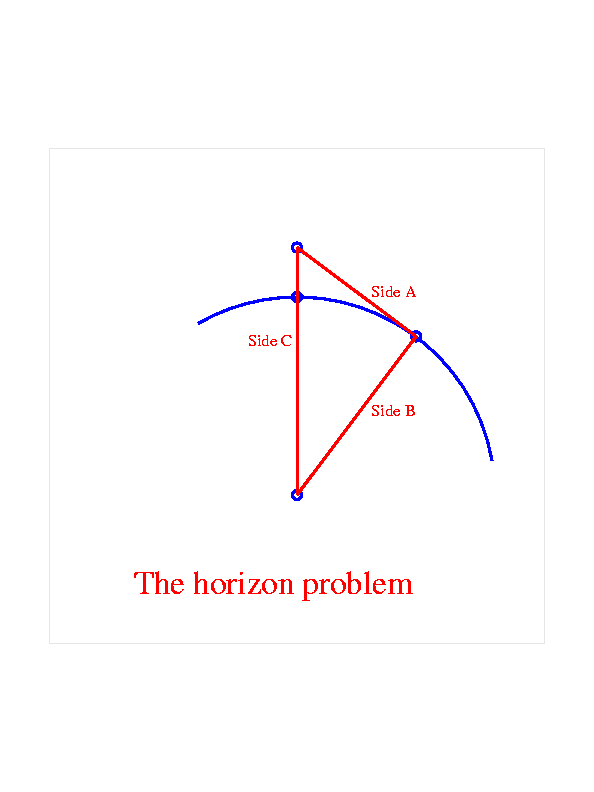
If we assume that Debbie has one eye, and it is on the top of her head, then the distance of her eye from the center of the earth is T+R miles, where R is the radius of the earth, which we are taking to be about 4,000 miles. Keep this in mind as line C.
Now we consider that Debbie is gazing at the horizon. Let us draw a line from her eye to the spot on the horizon she is staring at. This is line A and we will say it has length H. This line is tangent to the surface of the earth, that is, it just barely touches it at a single point.
Now let us draw line B, which starts at the point of tangency, (whatever it is that Debbie is staring at on the horizon), all the way down to the center of the earth. Obviously, line B has length R.

Because line A is tangent to the earth at this point, line A and line B are perpendicular to each other. Thus lines A, B and C form a right triangle. We may thus assert that:
( R + T )2 = R2 + H2
R2 + 2 * R * T + T2 = R2 + H2
2 * R * T + T2 = H2
H2 = 2 * R * T + T2
H = square root of ( 2 * R * T + T2 )
Now, for little Debbie standing on the earth, we can fill in the numbers:
H = square root of ( 2 * 4000 * 0.001 + 0.000001 )
= square root of ( 8.000001 )
= approximately 2.8 miles
Moreover, as long as the person (or giraffe or lighthouse) is relatively short
compared to 4000 miles, we can write a general approximate formula for the
distance to the horizon:
H (in miles) = 1.2 * square root of ( height in feet )
Thus, a 20 foot tall person would have a horizon of about 5.6 miles, and from a 500 foot
tall building you could see about 28 miles.
If you think about it, this means that two people who are each about 5 feet tall can just barely see each other at a distance of 5.6 miles. Moreover, a 500 foot tall person can just barely see a 5 foot tall person at a distance of 28 + 5.6 miles.