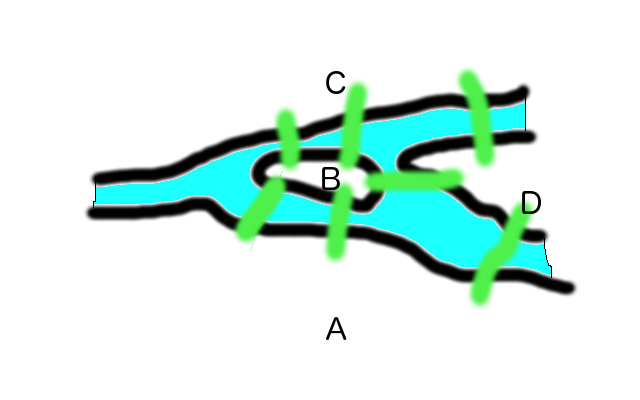
The good people of Koenigsberg, so the story goes, would take a Sunday promenade along the river banks of town and try their luck at a challenge that had been unsolved for decades. The town was situated at a spot where two rivers came together. Just below the river's meeting was a substantial island. Seven bridges joined the various sections of town, and the challenge was to take a tour that crossed every bridge exactly once. Some thought the tour had to begin and end at the same spot; but after seeing how hard the puzzle was, many people were willing to applaud a solution even if it started at one place and ended at another, as long as all the bridges were crossed just once.

Here we see the four sections of Koenigsberg, labeled "A" through "D", and the seven bridges. You are welcome to try to trace a suitable path that uses each bridge just once.
Somehow, Leonhard Euler heard of this puzzle, thought about it, and came up with an answer which also founded an entire new branch of mathematics, known as "graph theory". His argument can be suggested very briefly by considering the following experiment. Suppose we symbolize each of the land areas "A" through "D" by a large dot. Now if someone says they have a solution to the puzzle, they can put a pencil on one dot, and trace the path. But note that, as we draw the path, every time we "enter" a dot, we then "exit" it shortly thereafter. The exceptions to this rule are that on the first step, we exit the beginning node without leaving it, and on the last step, we enter the final node without exiting it. Therefore, every node will have an even number of entries and exits, except for the start and finish - unless the start and finish are the same, in which case that node is also even.
Now look at the map. There are four plots of land, which we called "nodes". If we can trace out a path over the bridges, then each bridge is a leg of our path, and so it must be true that either:
But Euler was wrong.
Any citizen of Koenigsberg could walk over each of the bridges exactly once, without help from anybody, without jumping into the river, or using a helicopter or digging a tunnel or using time travel. It's really quite simple.
It's a fact that a river has a beginning and an end. And if you are on one side of the river, and want to be on the other, and you don't mind walking a long long time, you can get to the other side without ever crossing water. So consider the following suggested solution to Euler's problem:
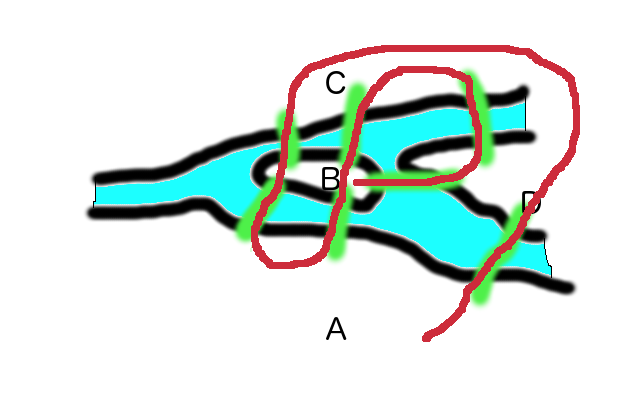
As you can see, our brave adventurer starts on the island B, and wanders around unremarkably, until arriving a second time on land mass C, where he might seem to have reached a dead end. But no, he simply walks and walks and walks around the river that only seems to be separating him from land mass D. It turns out that land masses C and D are actually connected, and so if he walks the right way, he'll reach D. Once there, he crosses the final bridge to land mass A and then marches to the town hall to demand the prize.
Now we really only "solved" the easier version of the Koenigsberg challenge. Can we use this approach to discover a path that ends where it began? Here, the answer must be no, because nothing we do about walking around the rivers will change the fact that there are five bridges on the island B, which means that any path using all bridges must begin or end on the island but not both.
Obviously, Euler was not really wrong...about the mathematical model. But it really is true that the actual puzzle of the bridges of Koenigsberg could have been solved, just as I say it could, without violating the rules. Essentially this is because, geographically, land masses A, C and D are really all part of a single connected land mass (i.e., Europe!), so that the model, looked at on a large enough scale, is misleading. This just goes to show that a mathematical model is an idealization, and true statements about the model are not necessarily true for the real world!