voronoi_diagram, just a sketch of some tools that are available for computing the Voronoi diagram of a set of points in the plane. Here, we are mostly concerned with ways of making pictures of such diagrams, or of determining the location of the vertices of the polygon around each generator.
To keep things simple, we'll only be concerned with 2D Voronoi diagrams, and we'll concentrate on a single small dataset of points whose coordinates are contained in the unit square. Here is a typewriter plot of the data:
2 . . . . . . . . . 9
. . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . . . . .
. . . 4 . . . . . . .
. . 3 . 5 . 7 . . . .
. . . . . . . . . . .
. . . . . . 6 . . . .
. . . . . . . . . . .
. . . . . . . . . . .
1 . . . . . . . . . 8
Here are the coordinates of the points:
0.0 0.0
0.0 1.0
0.2 0.5
0.3 0.6
0.4 0.5
0.6 0.3
0.6 0.5
1.0 0.0
1.0 1.0
One useful thing about this dataset is that I can tell you EXACTLY the shape of the Voronoi polygon around the point labeled 5. It consists of the four points (0.3,0.2), (0.5,0.4), (0.5,0.7), and (0.3,0.5), which form a sort of diamond around the point. This fact should help later on, when we are trying to understand the output of some of the programs.
In some cases, all we want to do is see a picture of the Voronoi diagram. We will see that there are a number of ways of doing that; however, even for this relatively simply job, there are some complications. Some plots don't show the rays to infinity. Some are line plots and some fill each region with color.
Often, we want to compute something based on the Voronoi diagram. Let's concentrate on one particular computation, determining the centroid of a Voronoi cell in 2D. To do this, we need to know the number of vertices in the cell and their locations. We also need to know their adjacency, that is, the order in which the vertices are placed around the generator.
We'll suppose that we start with g_num points in 2D, which we call generators. We have the coordinates of these points, available either as two lists g_x(1:g_num), g_y(1:g_num), or as a doubly-dimensioned array g_xy(1:2,1:g_num). We now suppose that our ideal program has computed the Voronoi diagram, and that it is willing to report this information using whatever data structure suits us.
The first piece of information we want is v_num, the total number of Voronoi vertices. Next, we want v_xy(1:2,1:v_num), the coordinates of the Voronoi vertices. Next, we want a vector g_degree(1:g_num) that contains the number of Voronoi vertices associated with each cell.
So far, it's been easy to think about the information and how to store it, but what about the lists of vertices? We'll want to be able to specify a generator I. From that, we know how to get the number of vertices, g_degree(i). Now let's suppose there's some big array g_face containing the lists, and that the list for generator I starts at g_start(i). Then we'll know that we have to read a total of g_degree(i) successive values to go around the polygon.
But how do we handle infinite polygons? These occur any time a generator G is part of the convex hull of the point set. In that case, the Voronoi region is a "polygon" with two semi-infinite sides. Perhaps the best way to handle this is to pretend that the region is essentially a polygon with one missing side. We imagine that there are "nodes at infinity". The degree of any Voronoi region with semi-infinite sides will be increased by 2. The list of vertices in g_face will be adjusted by adding one node at infinity to the beginning of the list, and one at the end. To indicate that these are special nodes, we will store them with a negative sign in the entries of g_face.
The number of nodes at infinity will be stored as i_num. The "directions" associated with these nodes will be stored in i_xy. To be clear about this, if a ray with direction i_xy(1:2,i) emanates from a Voronoi vertex v_xy(1:2,j), or if, in other words, finite vertex i is connected to the j-th vertex at infinity, then we intend that the corresponding ray is the set of points
v_xy(1:2,j) + s * i_xy(1:2,i)
for all nonnegative values s.
Thus, if we encounter a generator whose vertex list is
( -7, 11, 8, 4, -13),
we can draw the Voronoi region by starting with a line in the direction
stored in i_xy(1:2,7) that terminates at v_xy(1:2,11),
continue to vertices 8 and 4, and then draw a line from
v_xy(1:2,4) in the direction i_xy(1:2,13).
If the only thing we're interested in is a picture of the Voronoi diagram, then it's possible to greatly simplify the data that we need to store. Let's first not even try to handle the semi-infinite sides. Then really we just have a collection of line segments to describe. The most obvious approach would be to record
For our first plot, let's use the program VORONOI_PLOT. This program is invoked by a command like
voronoi_plot filename 2
where filename is the name of a text file containing the coordinates
of points in the unit square, and the "2" indicates that we're using the
usual L2 or Euclidean distance norm. We happen to have a usable input
file in diamond_02_00009.txt. Therefore
we issue the command
voronoi_plot diamond_02_00009.txt 2
which creates the output file diamond_02_00009_l2.ppm, an
ASCII PPM graphics file, which can be converted into the more
usable PNG format by the command
convert diamond_02_00009_l2.ppm diamond_02_00009_l2.png
The result of all this effort is here. You should be relieved to see
that the diamond-shaped Voronoi polygon is where I said it would be!
This picture shows us what the Voronoi diagram looks like. However, it doesn't actually work out the shape of the diagram. Instead, it simply discretizes the region, and then looks at each pixel and asks which generator is closest. In some ways, the program looks smarter than it is!
For our next plot, let's use the program PLOT_POINTS. This is an interactive program. We'll keep the interaction short though:
plot_points diamond_02_00009.xy
voronoi
quit
If we didn't include the input file name on the command line, we
could have indicated it directly to the program by a command like
read diamond_02_00009.xy
The voronoi command tells the program to compute the Voronoi
diagram and save it to an Encapsulated PostScript file; I used
convert to turn it into a PNG file.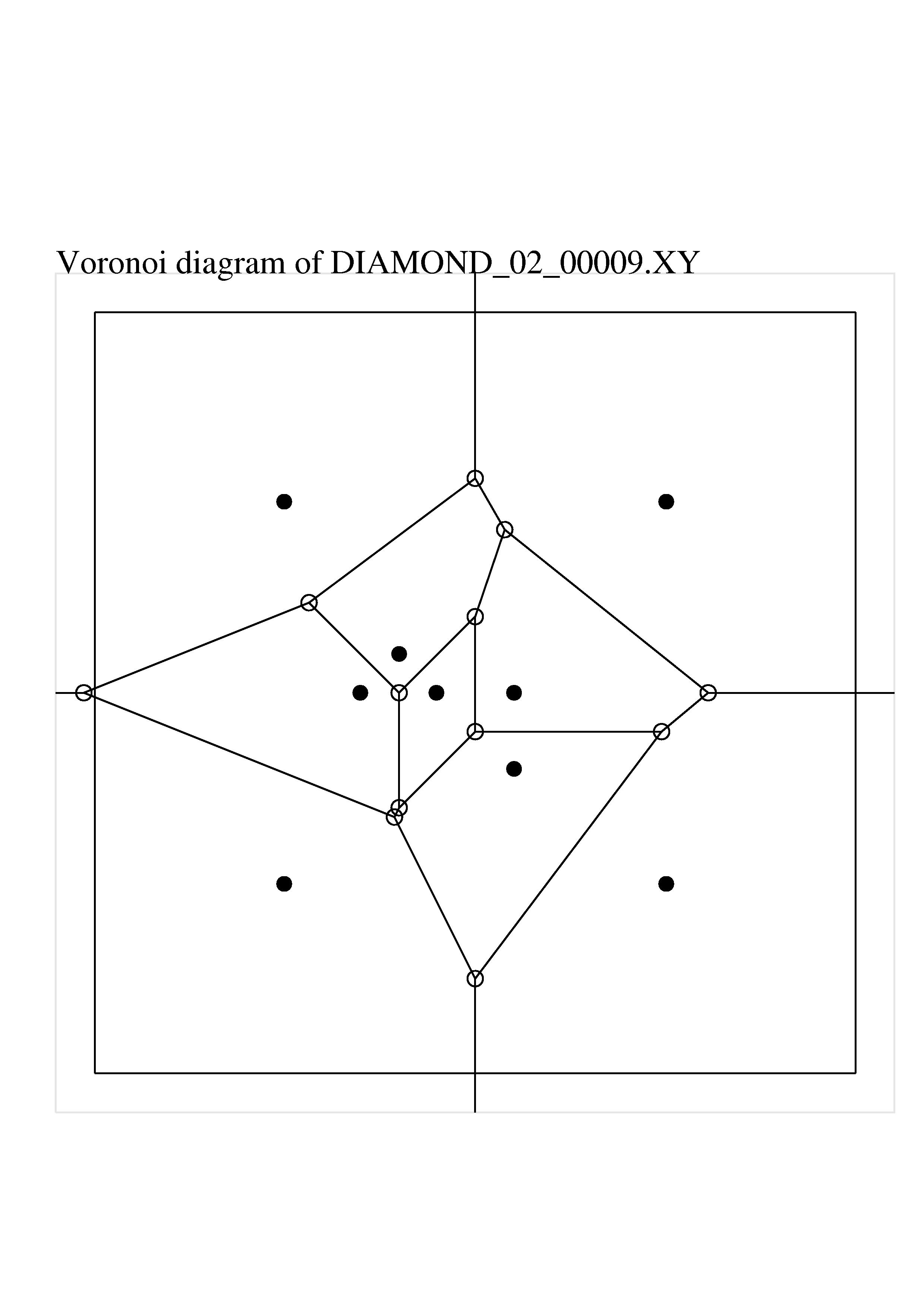
Actually, in order to get the program to include a larger area, I also gave the input command
box -0.5, -0.5, 1.5, 1.5
This is because I wanted to be sure the program demonstrated that it
knows about, and can draw, the parts of the Voronoi diagram that
extend to infinity.
This picture is less attractive than the one created by VORONOI_PLOT. However, notice that this program must be considerably smarter. The open circles indicate the location of Voronoi vertices, which the program must have worked out. It also must have worked out where the boundaries of the Voronoi diagram were. It also knows about, and handles correctly, the semi-infinite rays that are part of the Voronoi diagram of the generators that lie on the convex hull of the pointset.
It's not actually clear from this plot whether the program "knows" the sequence of Voronoi vertices that surround each generator. It could simply have a list of the line segments and rays that make up the diagram, which is enough to draw the picture (our eye takes care of figuring out the relationship between the generators and the vertices). However, for many applications, we will need to know the Voronoi vertex sequence, along with the complications that occur when a Voronoi region has semi-infinite sides.
I wrote the PLOT_POINTS program, but PLOT_POINTS relies for its Voronoi calculations on another program, which I didn't write, called GEOMPACK, which we'll get to eventually!
The Mathematica program includes a discrete mathematics package that can compute Voronoi diagrams. The following commands set up our data. (Note that we have to use names like gxy rather than g_xy because Mathematica uses the underscore character for other purposes!)
Clear[ points ]
Needs[ "DiscreteMath`ComputationalGeometry`" ]
gxy = { {0.0,0.0}, {0.0,1.0}, {0.2,0.5}, {0.3,0.6},
{0.4,0.5}, {0.6,0.3}, {0.6,0.5}, {1.0,0.0},
{1.0,1.0} }
ListPlot [ gxy, PlotJoined->False ]
{ vxy, gface } = VoronoiDiagram [ gxy ]
Here, the vxy array contains a list of objects, most of which are 2D coordinates, but a few of which (listed at the end) are actually infinite rays. The rays are described by the point where the ray starts, and a point further along the ray.
{
{-0.525, 0.500},
{ 0.064, 0.735},
{ 0.287, 0.175},
{ 0.300, 0.200},
{ 0.300, 0.500},
{ 0.500, -0.250},
{ 0.500, 0.400},
{ 0.500, 1.062},
{ 0.500, 0.700},
{ 0.576, 0.928},
{ 0.987, 0.400},
{ 1.112, 0.500},
Ray[{-0.525, 0.500}, {-1.525, 0.500}],
Ray[{ 0.500,-0.250}, { 0.500,-1.250}],
Ray[{ 0.500, 1.062}, { 0.500, 2.062}],
Ray[{ 1.112, 0.500}, { 2.112, 0.500}]
}
Each entry of the gface array contains the index of a generator (one of the original points), and the indices of the entries in vxy that form the Voronoi polygon around that generator. The actual form of gface returned is:
{
{ 1, { 6, 3, 1,13,14} },
{ 2, { 1, 2, 8,15,13} },
{ 3, { 1, 3, 4, 5, 2} },
{ 4, { 2, 5, 9,10, 8} },
{ 5, { 5, 4, 7, 9} },
{ 6, { 4, 3, 6,11, 7} },
{ 7, { 9, 7,11,12,10} },
{ 8, { 12,11, 6,14,16} },
{ 9, { 8,10,12,16,15} }
}
In order to get a plot of the data computed by VoronoiDiagram, we issue a command like this:
DiagramPlot [ gxy, vxy, gface ]
which will result in an image like this: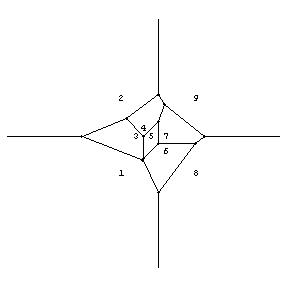
Thus, with a little Mathematica savvy, it is possible to draw a particular Voronoi polygon, determine if it is finite, find its centroid, and so on. This is the kind of information we want to know!
The MATLAB program is a very handy interactive program. It includes a number of computational geometry routines, and in particular, a voronoi command that makes the kind of plot we're interested in. With an eye to future work, let's first see if we can somehow get the data in the DIAMOND file into MATLAB. One way to do this is to use the MATLAB versions of the TABLE_READ routine. If we've copied the file table_read.m, then we can tell MATLAB to get our file as follows:
g_xy = table_read ( 'diamond_02_00009.xy' );
Then we can make a Voronoi plot easily with the command
voronoi ( g_xy(:,1), g_xy(:,2) );
The result can be exported directly from MATLAB to a JPEG file,
and looks something like this:
Although MATLAB is flexible, fast, and easy to use, the output of the VORONOI command isn't quite what we want. First of all, we're only getting a picture, not data. And in fact, if you save the output of the command:
[ l_x, l_y ] = voronoi ( g_x, g_y );
you get just a set of data describing the line segments to be drawn.
In other words, l_x is an array of 2 rows and l_num columns,
where l_num is the number of (finite) line segments in the
Voronoi diagram.
Thus, although the voronoi command plots the diagram, we could do this ourselves via the commands:
[ l_x, l_y ] = voronoi ( g_x, g_y );
[ dummy, l_num ] = size ( l_x );
for ( l = 1 : l_num )
plot ( l_x(1:2,l), l_y(1:2,l) )
end
But if we're interested in how the line segments are grouped to make polygons, we're out of luck. There is no information returned by the command.
One drawback of the voronoi command is that, by default, it frames the plot within the convex hull of the original set of points. This means, especially for small point sets, that a fair chunk of the interesting part of the picture is not shown, including some Voronoi vertices.
Moreover, the Voronoi diagram always includes some semi-infinite sides, but the voronoi command does not compute or plot these. If the semi-infinite edges aren't drawn, you miss some important aspects of the picture.
In order to address these problems, it is necessary to work with a more sophisticated MATLAB command called voronoin.
For serious applications (including datasets in 3D or higher dimension), MATLAB includes a more general function called VORONOIN.
[ v_xy, g_face ] = voronoin( g_xy )
Now v_xy is a list of vertex coordinates, and the I-th entry of the
vector cell-array g_face is a list of the indices of Voronoi
vertices (whose coordinates are in v_xy) that comprise the
Voronoi polygon around the I-th generator.
Because g_face is not a simple matrix, it may be of interest to see how to display the entries:
for ( i = 1 : length ( g_face ) )
disp ( g_face{i} );
end
(Note that g_face is indexed by curly braces!) For 2D
problems, the vertices in g_face are listed in adjacent order.
Thus, continuing this example, we could display the 3rd Voronoi cell by extracting the 3rd row of g_face, using it to index v_xy and drawing the convex hull of the result:
v3_x = v_xy ( g_face{3}, 1 );
v3_y = v_xy ( g_face{3}, 2 );
k = convhull ( v3_x, v3_y );
plot ( v3_x(k), v3_y(k) );
If we replace the plot command by a fill command to create a filled polygon, and add a scatter command to display the original points, we can see a plot of the individual Voronoi cell:
fill ( v3_x(k), v3_y(k), 'r' );
hold on;
scatter ( g_xy(1,:), g_xy(2,:) );
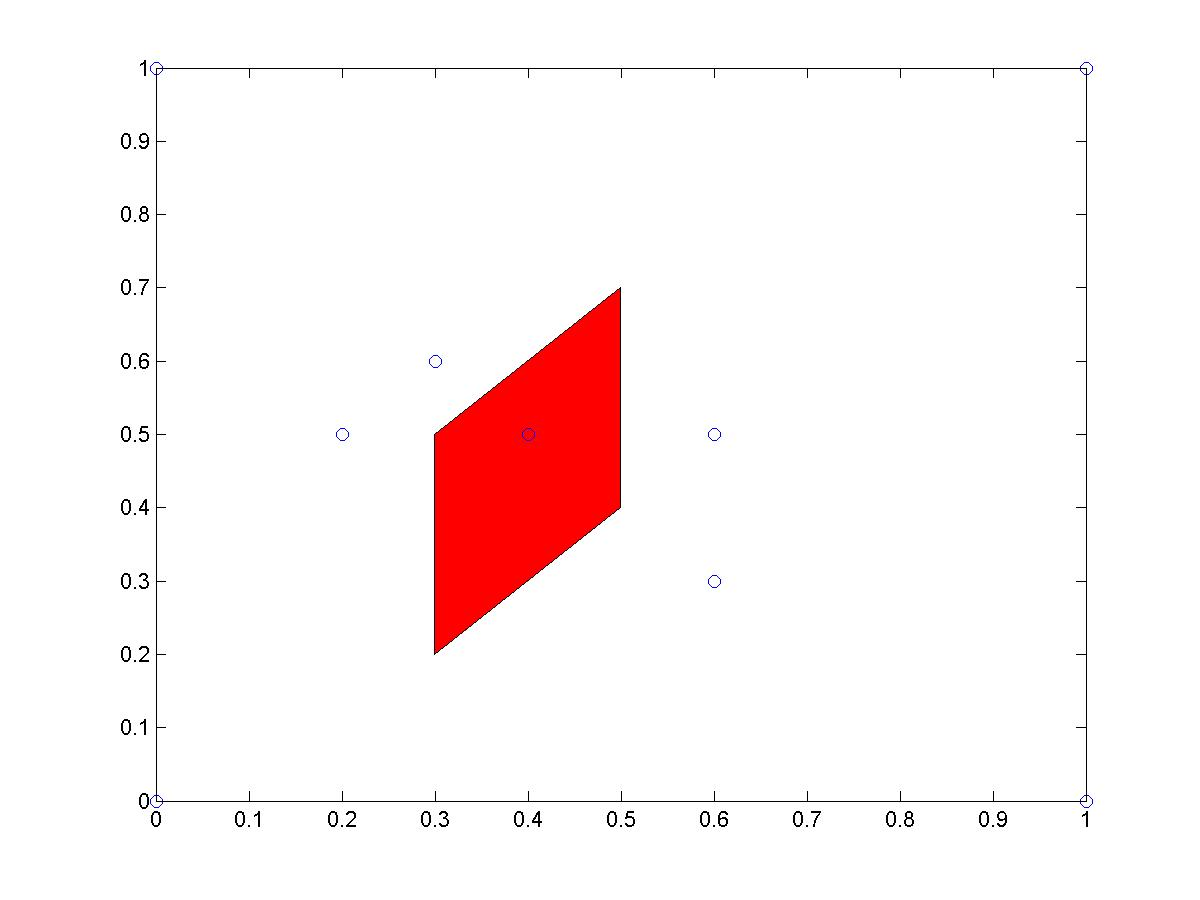
Unfortunately, there is not enough information provided in the v_xy and g_face to take care of the semi-infinite Voronoi regions. All we are told in g_face is that such polygons begin and end with the same single point at infinity. While this tells us something (the polygon is semi-infinite), it does not tell us how to draw the ray that denotes the boundary between this semi-infinite polygon and its (also semi-infinite) neighbor.
The online MATLAB documentation for VORONOIN claims that it is delivering this information from an internal copy of the QHULL program, and that help with the semi-infinite ray directions can be gotten by adding an appropriate parameter, but this "documentation" has failed to help me! My few attempts to figure out where this data is hidden have brought nothing so far.
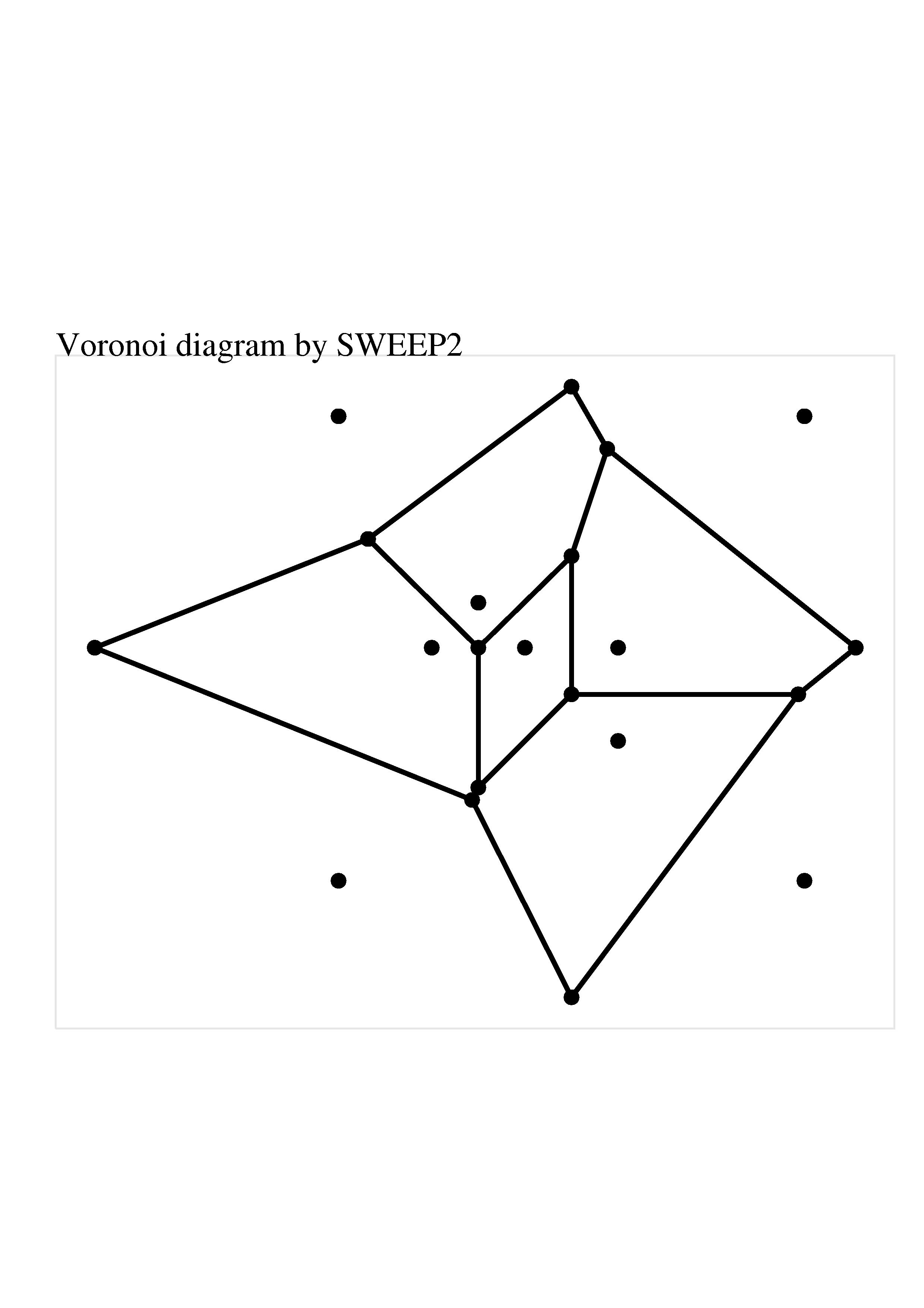
Steve Fortune wrote a C program called SWEEP2 which can produce the Voronoi diagram or Delaunay triangulation of a set of points. To compute the Voronoi triangulation, the point set must be in a file, say points.txt, with each line containing the coordinates of a single point. Issuing the command
sweep2 < points.txt > points_del.txtwill create an output file containing information defining the Voronoi diagram.
The description of the Voronoi diagram is fairly complicated. There are four kinds of records in the output file:
For the diamond dataset, the SWEEP2 program produced the output file:
s 0.000000 0.000000
s 1.000000 0.000000
l 1.000000 0.000000 0.500000
s 0.600000 0.300000
l 1.000000 -0.750000 0.687500
v 0.500000 -0.250000
l 1.000000 0.500000 0.375000
s 0.200000 0.500000
l 0.400000 1.000000 0.290000
s 0.400000 0.500000
l 1.000000 -1.000000 0.100000
s 0.600000 0.500000
l 0.000000 1.000000 0.400000
v 0.287500 0.175000
e 2 1 0
l 1.000000 -0.500000 0.200000
v 0.300000 0.200000
e 6 1 2
l 1.000000 0.000000 0.300000
v 0.500000 0.400000
e 4 2 3
l 1.000000 0.000000 0.500000
s 0.300000 0.600000
l 1.000000 1.000000 0.800000
v 0.300000 0.500000
e 7 4 2
l -1.000000 1.000000 0.200000
v 0.987500 0.400000
e 5 3 5
e 1 0 5
l -0.800000 1.000000 -0.390000
v 0.500000 0.700000
e 10 4 6
e 8 6 3
l 1.000000 -0.333333 0.266667
s 0.000000 1.000000
l -0.400000 1.000000 0.710000
s 1.000000 1.000000
l 0.800000 1.000000 1.390000
v 0.064286 0.735714
e 9 7 4
l -0.750000 1.000000 0.687500
v 1.112500 0.500000
e 11 5 8
l 0.000000 1.000000 0.500000
v -0.525000 0.500000
e 3 9 1
e 13 9 7
l 0.000000 1.000000 0.500000
v 0.576316 0.928947
e 12 6 10
e 14 10 8
l 1.000000 0.571429 1.107143
v 0.500000 1.062500
e 15 7 11
e 18 11 10
l 1.000000 0.000000 0.500000
e 17 -1 9
e 19 -1 11
e 16 8 -1
e 0 0 -1
The output from the SWEEP2 may seem excessive and obscure, but it has some very interesting properties. Let us begin by noting that the s records in the output do not occur in the same order as they were input. They have been sorted by the y coordinate:
#0: s 0.000000 0.000000
#1: s 1.000000 0.000000
#2: s 0.600000 0.300000
#3: s 0.200000 0.500000
#4: s 0.400000 0.500000
#5: s 0.600000 0.500000
#6: s 0.300000 0.600000
#7: s 0.000000 1.000000
#8: s 1.000000 1.000000
Now notice that, after the first two sites have been output, the next
item in the file is a "line" object,
l 1.000000 0.000000 0.500000
which indicates that line #0 has the equation
1.0 * x + 0.0 * y = 0.5
which is the perpendicular bisector of the line between sites #0 and #1.
The program has actually only considered the first two points, and now
"knows" that it may need the perpendicular bisector between them.
After reading another site, it outputs line #1, and then outputs Voronoi vertex #0. The reason that the code can output this Voronoi vertex is that it knows the points have been sorted by y coordinate, and so part of the Voronoi diagram is actually now mainly understood. It turns out that you can be sure of the location of Voronoi vertices sooner than you can be sure of the extent of Voronoi edges, (partly because you have to know where two vertices are to specify one edge), so it's not until six sites have been processed, and two vertices determined, that we can determine the first Voronoi edge. (And in some examples, it might be the case that many Voronoi vertices would be determined before even one Voronoi edge could be set.)
This incremental approach to processing the data keeps the internal memory requirements low and speeds the algorithm. Of course, it also explains why the output of the four kinds of records occurs in a jumble, as you go.
I have drafted a program SWEEP2_VORONOI_EPS, which is able to read the Voronoi diagram information, and construct an Encapsulated PostScript file containing an image of the diagram. The program has a few flaws. Although SWEEP2's data file does include information about the semi-infinite Voronoi edges, I have not yet done the work necessary to draw them. And the plot by default includes all points and vertices, so the SWEEP2 test dataset does not have a very nice plot, because the data is entirely in the unit square, except for a single vertex with x coordinate -13. This causes the plot to be very badly scaled.
Here is the Voronoi plot created for the diamond data set:

Barry Joe wrote several versions of a FORTRAN package called GEOMPACK, which computes the Voronoi diagram or Delaunay triangulation using fairly simple data types. Most versions of the package contain many more routines than you need. The fundamental routine is called either DTRIS or DTRIS2 or RTRIS or RTRIS2; the D or R was used to distinguish double and single precision versions, and the 2 was used after Barry Joe developed 3D versions of the code as well.
I have a version of this program, which I converted to FORTRAN90, in the directory ../f_src/geompack/geompack.html
I have a second version of a subset of this program, which I converted to C++, in the directory ../../cpp_src/geompack/geompack.html While it is much less extensive than the FORTRAN version, it includes the RTRIS2 routine, and so can do a Delaunay triangulation.
The RTRIS2 code computes the Delaunay triangulation directly from the coordinates of a point set.
The RTRIS2 code computes the Delaunay triangulation, but not the Voronoi diagram. However, since these two objects are so closely related, it is possible to get from one to the other. I did this once already in PLOT_POINTS, and here will sketch out what has to be done.
Start with g_num points with coordinates in g_xy. To generate the Delaunay triangulation, we call
call rtris2 ( g_num, g_xy, v_num, nod_tri, tnbr )
Warning! It is important to note that RTRIS2, as written, sorts the point coordinates, and on exit, returns the sorted point coordinates. This can be very disruptive if you are not aware of it! I find this fact so unpleasant that, in many cases, I have modified RTRIS2 so that it works with an index sort vector instead, producing the same output as before, except that the point coordinates are not modified. Before I made this change, I repeatedly encountered severe problems, such as making a plot using the old node coordinates, but with triangulation data that assumed the node coordinates had been shuffled by the sorting. The result is a meaningless spaghetti plot! And this hardens my belief that a subroutine's arguments should be INPUT or OUTPUT but NOT both!
The number of Voronoi vertices (and Delaunay triangles) is returned as v_num; for our sample problem, this value is v_num=12.
The array nod_tri(1:3,v_num) lists the three generators that form the vertices of each Delaunay triangle; for our sample problem, this array looks like:
1 2 1 3
2 3 1 6
3 2 3 4
4 4 3 5
5 7 4 5
6 5 3 6
7 7 5 6
8 9 4 7
9 6 1 8
10 7 6 8
11 7 8 9
12 2 4 9
The array tnbr indicates, for each Delaunay triangle (or Voronoi vertex) the index of the neighboring triangle (or vertex) along each side. However, some triangles don't have a neighbor on a particular side (and correspondingly, some Voronoi vertices don't have a finite Voronoi neighbor). In such cases, the corresponding entry is a negative value:
1 -1 2 3
2 1 9 6
3 1 4 12
4 3 6 5
5 8 4 7
6 4 2 7
7 5 6 10
8 12 5 11
9 2 -2 10
10 7 9 11
11 10 -3 8
12 3 8 -4
(The actual negative values returned by RTRIS2 are different, and somewhat
arbitrary. I've made them consecutive for simplicity.)
This is the data we are going to have to manipulate in order to determine the Voronoi information.
The easiest thing to do is to compute the circumcenter of each Delaunay triangle, because these are the vertices of the Voronoi polygons!
do v = 1, v_num
call triangle_circumcenter_2d (
g_xy(1,nod_tri(1,v)), g_xy(2,nod_tri(1,v)),
g_xy(1,nod_tri(2,v)), g_xy(2,nod_tri(2,v)),
g_xy(1,nod_tri(3,v)), g_xy(2,nod_tri(3,v)),
v_xy(1,v), v_xy(2,v) )
end do
Now, to draw the Voronoi diagram, look at each Delaunay triangle, and each edge of that Delaunay triangle. If there is a neighboring triangle along that edge, then connect the two circumcenters. If there is no neighbor, then this is an infinite edge, so you can extend a line indefinitely from the circumcenter through that side in the outward normal direction.
do v = 1, v_num
do j = 1, 3
k = tnbr(j,v)
if ( 0 < k ) then
connect v_xy(1:2,v) to v_xy(1:2,k)
else
determine outward normal N to the triangle edge, and draw
a ray from v_xy(1:2,v)
end if
end do
end do
Going through this procedure now, I recall that it took me a long time to work it out from the data that GEOMPACK supplies. Also, I realize that we don't actually have a convenient data structure that lists the Voronoi vertices that form a particular Voronoi diagram. You'd have to examine every Delaunay triangle and see whether your node of interest was one of the three vertices of the triangle. The index of that triangle is also the index of the circumcenter. From that triangle, you can look to the "left" and "right" to find the previous and next vertices in the Voronoi polygon, and thus either go all the way around a finite polygon, or come to the ends of an infinite one. Well, it's doable, but I didn't do it!
As mentioned above, RTRIS2 and its underlying routines are available in the FORTRAN90 code GEOMPACK. I have also extracted these routines for use in the PLOT_POINTS program, in order to compute and display Delaunay triangulations and Voronoi diagrams.
I also put a copy of the routines in the FORTRAN90 GEOMETRY library, along with many routines for printing out the arrays associated with the triangulation. The test code for GEOMETRY includes a setup of the DIAMOND dataset.
I have just recently worked out a C++ version of RTRIS2, made available in the C++ GEOMETRY library. This does not yet include the extra routines for printing out the triangulation arrays The test code includes a setup of the DIAMOND dataset.
I decided that we needed a good FORTRAN code that returns the Voronoi diagram data. I based the code on the RTRIS2 routines from GEOMPACK, and used the ideas that had worked in PLOT_POINTS to convert the Delaunay information to Voronoi data. However, PLOT_POINTS was only drawing a picture, so it didn't need to be construct a full data structure description of the Voronoi diagram. For my purposes, I needed to figure out a data structure that would encapsulate the Voronoi diagram, and allow me not only to plot the diagram, but to record all the polygonal degree and neighbor information. If this was done properly, then it would be easy, for instance, to determine if any Voronoi cell was finite, and to compute the area or centroid of any finite cell.
The program is interactive. It assumes that the user has prepared a list of the point coordinates, in the form of an XY data file, so that the program invocation looks something like
table_voronoi diamond.xy
The program counts g_num, the number of generators, and stores the coordinates in the array g_xy(1:2,1:g_num). The program then calls GEOMPACK to compute the Delaunay triangulation, and from that data computes the following Voronoi quantities:
For our sample problem, the information for the g_num=9 generators is:
G G_DEGREE G_START G_FACE
1 5 1 -14 9 2 1 -13
2 5 4 -13 1 3 12 -16
3 5 7 1 3 4 6 2
4 5 12 3 12 8 5 4
5 4 17 4 5 7 6
6 5 21 2 6 7 10 9
7 5 26 5 8 11 10 7
8 5 31 -15 11 10 9 -14
9 5 34 -16 12 8 11 -15
Here, the negative entries indicate fictitious nodes at infinity, whose
directions are stored in i_xy.
For the v_num=12 Voronoi vertices,
V V_XY
1 -0.525 0.500
2 0.287 0.175
3 0.064 0.735
4 0.300 0.500
5 0.500 0.700
6 0.300 0.200
7 0.500 0.400
8 0.576 0.928
9 0.500 -0.250
10 0.987 0.400
11 1.112 0.500
12 0.500 1.062
and, with i_num = 4, the "directions" of the fictitious nodes at
infinity are
I I_XY
1 -1.0 0.0
2 0.0 -1.0
3 1.0 0.0
4 0.0 1.0
(You could also relabel the fictious nodes at infinity with the values
13, 14, 15 and 16, and stick the four values in I_XY onto the
end of the V_XY array, if you could keep clear that these four values
are really directions, not locations!)
Note that, to draw the rays that form part of the boundary of the unbounded regions, you look for a negative node in G_FACE. Suppose we are working on the region associated with the first generator. Then the first negative index we encounter is -14. Make it positive, and subtract the value of V_NUM to get its index of 2. This gets you the direction (0.0,-1.0) in the I_XY array.
Now look for the predecessor or successor of 14 in the G_FACE array (Negative entries only occur as the first or last entries in a list). In this case, -14 is followed by 9. So to draw this portion of the boundary, you start at node 9, and draw as much of the direction
( v_xy(1,9) + s * i_xy(1,2), v_xy(2,9) + s * i_xy(2,2) )
as will fit in your picture. For region 1, the other ray is associated with
the negative node -13, we move to its finite predecessor in the list, vertex 1,
and draw a line from there in the direction stored in I_XY,
entry |-13|-12 = 1. There, wasn't that easy?
I understand that the set of data structures and conventions described here is not the cleanest. It is also true that the method by which I "massage" the Delaunay data coming out of GEOMPACK is inefficient and very slow if the number of generators is large. But I do believe that I've tracked down the data necessary to plot and more importantly analyze the Voronoi regions, including the often-neglected unbounded regions.
Robert Renka has published a number of algorithms in ACM TOMS. In particular, TRIPACK (ACM TOMS Algorithm #751) computes the Delaunay triangulation of a set of points in the plane. From the remarks above about GEOMPACK, it should be clear that this information is enough to compute the Voronoi diagram.
Another algorithm published by Renka is STRIPACK, (ACM TOMS Algorithm #772). This is essentially the same as TRIPACK, except that the points lie on a sphere. It should (eventually) be clear that the information about a Delaunay triangulation on a sphere is enough to work out the Voronoi diagram, with the added feature that there are no infinite regions.
TRIANGLE is Jonathan Shewchuk's C program for producing meshes, Delaunay triangulations and Voronoi diagrams. You can look at my local copy of TRIANGLE.
TRIANGLE requires a slightly different input file from the XY format we have used elsewhere, called the "node" format. The '#' comment lines in our XY format are still acceptable, but there must be one line that specifies the number of nodes (and some other information) and each line of coordinate data must begin with the index of the vertex. A version of our DIAMOND data looks something like this:
# diamond_02_00009.node
9 2 0 0
1 0.0 0.0
2 0.0 1.0
3 0.2 0.5
4 0.3 0.6
5 0.4 0.5
6 0.6 0.3
7 0.6 0.5
8 1.0 0.0
9 1.0 1.0
If we now invoke TRIANGLE with the "-v" (for Voronoi) option:
triangle -v diamond_02_00009.node
it quickly creates four files:
The file diamond_02_00009.1.v.node corresponds to our data structure g_xy. It includes the four corners of the diamond, so we know that's right:
12 2 0 0
1 -0.525 0.500
2 0.300 0.500
3 0.500 1.062
4 0.064 0.735
5 0.287 0.175
6 0.987 0.400
7 0.500 -0.250
8 0.576 0.928
9 0.500 0.400
10 1.112 0.500
11 0.500 0.700
12 0.300 0.200
# Generated by triangle -v diamond_02_00009.node
(I've reformatted this file so that the data lines up, and is all printed
to three decimals, just to make comparisons easier.)
The file diamond_02_00009.1.v.edge corresponds to our data structure l_vert. However, it lists twenty edges, which includes the four infinite edges. These are marked by the use of a format in which the second node index is -1, followed by two values which are interpreted as the direction of the infinite ray. Thus, the 9th edge starts at Voronoi vertex 3, and then extends infinitely in the direction (0,1), an upward vertical ray.
20 0
1 1 5
2 1 4
3 1 -1 -1 0
4 2 4
5 2 12
6 2 11
7 3 4
8 3 8
9 3 -1 0 1
10 5 7
11 5 12
12 6 7
13 6 10
14 6 9
15 7 -1 0 -1
16 8 10
17 8 11
18 9 11
19 9 12
20 10 -1 1 0
# Generated by triangle -v diamond_02_00009.node
Again, we have lots of information, but not, apparently, an explicit list of the Voronoi vertices that surround each generator. To determine the Voronoi vertices around node 5, then, we need to read the Delaunay triangulation edge list (diamond_02_00009.1.ele) for triangles that include node 5, which turns out to be triangles 2, 9, 11, and 12. The corresponding Voronoi vertices are listed in diamond_02_00009.1.v.node. If we really want to list the vertices in order, to produce a traversal of the polygon, then we need to look at the Delaunay triangles and find matching pairs of edges.
TRIANGLE includes another program called SHOWME which can be used to make an X-window display of a mesh, or to save an image as a PostScript file.
To see the Voronoi diagram we just created, it is only necessary to type
showme diamond_02_00009.1.v.edge
I save the image as a PostScript file, and converted that to JPEG using
GSView.
The QVORONOI program is part of the QHULL package, which has a home page at http://www.thesa.com/software/qhull/.
QVORONOI is an interactive program that reads an input file, computes the Delaunay triangulation, determines the Voronoi diagram, and either prints a summary, or outputs the information to a file, based on command line switches.
The format for the pointset coordinate file is fairly simple. Lines beginning with a nonnumeric character are treated as comments. The first noncomment line must contain the spatial dimension; the second line gives the number of points, and each subsequent line lists the coordinates of a single point. Thus, our standard diamond example file would be slightly modified from "xy" format to a new format we could call "qxy", which might look like this:
# diamond_02_00009.qxy
#
2
9
0.0 0.0
0.0 1.0
0.2 0.5
0.3 0.6
0.4 0.5
0.6 0.3
0.6 0.5
1.0 0.0
1.0 1.0
The command line switch "p" requests that the coordinates of the Voronoi vertices be listed (which we've called V_XY). Thus, the command
qvoronoi diamond_02_00009.qxy p
results in the output:
2
12
0.500 -0.250
-0.525 0.500
0.287 0.175
0.300 0.200
1.112 0.500
0.987 0.400
0.500 0.400
0.064 0.735
0.300 0.500
0.500 1.062
0.500 0.700
0.576 0.928
which we recognize as a proper list of the Voronoi vertices, with the
addition of the two initial lines that given the dimension and number.
(For clarity, I reformatted this data so that it lined up and only
listed three decimal places.)
The command line switch "FN" requests that, for each generator, the sequence of Voronoi vertices be listed. Thus, the command
qvoronoi diamond_02_00009.qxy FN
results in the output:
9
4 2 0 -1 1
4 9 -1 1 7
5 8 3 2 1 7
5 11 9 7 8 10
4 10 6 3 8
5 6 3 2 0 5
5 11 4 5 6 10
4 5 0 -1 4
4 11 4 -1 9
where the "9" indicates the number of generators, and, in the subsequent
lines, the first value is the number of vertices (what we called
G_DEGREE), followed by the list of vertices (which we've called
G_FACE). If the region is unbounded, then a single value of -1
in the vertex list indicates the vertex at infinity.
The command line switch "o" requests that an OFF file be created, containing the information about the Voronoi diagram, and suitable for display by the GEOMVIEW program. The form of this OFF file is:
2
13 9 1
-10.101 -10.101
0.500 -0.250
-0.525 0.500
0.287 0.175
0.300 0.200
1.112 0.500
0.987 0.400
0.500 0.400
0.064 0.735
0.300 0.500
0.500 1.062
0.500 0.700
0.576 0.928
4 3 1 0 2
4 10 0 2 8
5 9 4 3 2 8
5 12 10 8 9 11
4 11 7 4 9
5 7 4 3 1 6
5 12 5 6 7 11
4 6 1 0 5
4 12 5 0 10
Most of this information makes sense. The initial "2" says that the data
is 2-dimensional. The next line says there are 13(?) nodes and 9 faces
and 1(?) edge. There are 13 nodes because the program adds the bogus point
(-10.101, -10.101) as a standin for infinity, and the edges are listed as
1 because this piece of information is no longer used, but a dummy value
must be supplied. Notice that the vertex indices range from 0 to 12,
with 0 being the point at infinity.
This data file is supposed to be usable as input to the GEOMVIEW program. However, it was only after a certain amount of work that I was able to get the program installed, it did not accept the input file, (the initial "2" had to be deleted, and a magic "OFF" inserted there) and after I "fixed up" the input file, (by adding a Z coordinate of 0 to each point) the plot was unacceptable; after I massaged the data (by moving the point at "infinity" to zero and removing the point at infinity from all the polygons), I did see the diamond-shaped region, but of course without the infinite edges. But when I tried to save an copy of this poor image in PPMA format, the program froze and I had to exit with nothing. My initial verdict on viewing QVORONOI OFF files with GEOMVIEW is therefore, don't bother!
In some frustration, I spent some time sketching out a program called TABLE_VORONOI to compute enough information to get the Voronoi diagram right. What I came up with is a program that doesn't actually know how to store this information, but prints it out. That makes it impractical for big calculations; it's just a start. However, I just didn't have the time to work out how to set up an array to handle the information, especially since we're tracking polygons and semi-infinite polygons of varying degree.
However, I was able to see that the things I wanted are computable.
The program begins with the pointset, of which a typical element is a point G. Each G generates a Voronoi polygon (or semi-infinite region, which we will persist in calling a polygon). A typical vertex of the polygon is called V. For the semi-infinite regions, we have a vertex at infinity, but it's really not helpful to store a vertex (Inf,Inf), since we have lost information about the direction from which we reach that infinite vertex. We will have to treat these special regions with a little extra care.
We are interested in computing the following quantities:
So if we have to draw a semi-infinite region, we start at infinity. We then need to draw a line from infinity to vertex #2. We do so by drawing a line in the appropriate direction, stored in I_XY. Having safely reached finite vertex #2, we can connect the finite vertices, until it is time to draw another line to infinity, this time in another direction, also stored in I_XY.
A Centroidal Voronoi Tessellation (CVT) is a set of generators with the special property that each generator is the centroid of its Voronoi cell. It is not easy in general to compute a CVT; there is an implicit relationship between the location of the generators and the shape of their Voronoi regions. However, a CVT with a given number of generators, confined to a given region, can be approximated by one of several kinds of iterations. Aside from requiring a bounded region, some iterations also need to compute the area and centroids of the Voronoi cells. Other iterations are probabilistic, and can approximate these quantities using sampling.
For a CVT calculation, we normally assume that the generators and all the points of interest are restricted to a finite bounding region. We can still generate the full Voronoi diagram, with some infinite cells, but we only consider the intersection of this diagram with the bounding region. Since each generator is within the bounding region, or at least on its boundary, and finitely separated from all other generators, it will never have an empty Voronoi cell, even after we discard the part outside the bounding region.
The bounding box is crucial because, as part of the computation, we need to compute the centroids of the individual Voronoi cells. If the region is infinite, then some of our centroids will also be infinite and the algorithm will break down. The fact that each generator's Voronoi cell will have some positive area within the bounding region also keeps the algorithm operating smoothly.
The exact CVT methods require the explicit construction of the Voronoi cells, and the computation of their areas and centroids. If the region were infinite, then the Voronoi cells would always have polygonal sides, so the area and centroid calculations are easy. But with a bounding region, we now face the situtation that some Voronoi cells will have the boundary of the region as one of their sides. If the shape of this bounding curve is arbitrary, then we may have a difficult time determining the shape, area, and centroid of the corresponding Voronoi cell. For convenience, let us assume that the bounding region itself is polygonal. We might further assume that it is convex, or has sides that are always along coordinate directions. In the simplest case, we may assume that the bounding region is actually an M-dimensional interval, or generalized box.
In this simplest case of an M-dimensional interval for the bounding region, it is usually possible to determine the shape of the intersection of any Voronoi cell with the bounding region. For instance, in two dimensions, the shape of such a Voronoi cell can easily be plotted. We simply start with the line segment or semi-infinite ray that forms one side of the cell. We then consider each side of the bounding box, and ask whether the given segment or ray intersects that side. If it does, then we need to modify the line segment or ray appropriately, by chopping off any portion that extends past that side of the box. Once all four (or 2*M in general) sides of the box have been considered, we can draw what's left of the line segment or ray.
The program PLOT_POINTS uses this simple method in order to display the portion of a Voronoi diagram that will fit in the current plot box.
It's actually a little harder to compute the area of the cell, rather than just to draw it. To do so, we consider the fact that (at least for our simple cases) the bounding box is convex, and the (original, unbounded) Voronoi cell will be convex, so the intersection of these two will also be convex. This means we can find the shape of the Voronoi cell by starting with the bounding region, and then taking its intersection with the halfplanes defined by each of the bounding lines of the original Voronoi cell. Once you think of the problem this way, you should be able to organize the calculation and the data structure that you would need. Since we end up with a polygonal region, we know that our problem is reduced to determining the area and centroid of a polygonal region.
There are several iterative procedures that can be used to compute a CVT. They each begin from some initial set of generators that lie in the region. In each step of the iteration,
In 2D, it is possible to carry out each step of this procedure in what is essentially an exact manner. (We're saying here that each step of the iterative procedure may be done in an exact manner. Each step still will produce only an approximation of a CVT. We're just saying that by following this procedure, we'll have made the best approximation that is possible.)
What we are saying is that, given a set of generators, it is possible to determine the location of the Voronoi vertices precisely, to restrict the Voronoi cells to the given finite region, and, assuming the finite region did not introduce any complexity to the shape of the cells, to compute the area and first moments of the Voronoi cells, thus arriving at the centroids.
It is also possible, when using some programs, and with rather more overhead, to carry out this process in 3D as well. There are some programs that will compute the arrangement of vertices and polygonal faces that form each Voronoi polyhedron. Because of the complexities of 3D geometry, it could be a bit more difficult than in the 2D case to determine the form of the Voronoi cells when restricting them to the finite region of interest. If these cells remain polyhedra, then it is possible to compute the volume and first moments of the Voronoi cells, thus arriving at the centroid.
In higher dimensions, it is not really feasible to pursue this exact approach, and instead, approaches using probablistic sampling must be applied in order to estimate the volume and centroid and carry out each step of the CVT iteration.
Still, the 2D and 3D cases are fairly common, so it should be of interest to note how one can compute areas, volumes and centroids. These matters are now briefly considered.
In 2D, the area of a polygon P with N vertices is easy to compute. We assume we are given the coordinates of the vertices, and we may assume that the polygon is not degenerate (in particular, that the polygon is not folded over on itself.)
The simplest approach is to triangulate the polygon and add up the areas; if we aren't particular, we can choose vertex N as the base, and then consider the N-2 triangles formed by the base vertex plus consecutive pairs of vertices from (1,2) through (N-2,N-1):
Area ( P ) = sum ( T in P ) area ( T )
where the area of a triangle is easily computed:
Area ( T ) = 1/2 * ( x1 * ( y2 - y3 ) + x2 * ( y3 - y1 ) + x3 * ( y1 - y2 ) )
(In the formula for the triangle, the indices 1, 2, and 3 simply indicate
the three vertices of the triangle, and don't refer to the original numbering
of the vertices of the polygon.)
A second formula for polygonal area is simply
Area ( P ) = 1/2 * sum ( 1 <= i <= N ) x(i) * ( y(i+1) - y(i-1) )
where we "wrap around" the indices when they exceed the legal range.
In MATLAB, if the coordinates of a polygon are stored in the column vectors p_x and p_y, then the area of the polygon can be found with the command
area = polyarea ( p_x, p_y )
In some cases, instead of having the vertices of the Voronoi polygon around generator G, we might have the list of generators that are Delaunay neighbors. This is actually a fairly common situation. It is still possible to compute the area of the Voronoi polygon directly from this information, using a formula given in Spatial Tesselations [Okabe].
The x coordinate of the centroid of a 2D region P is
centroid_x ( P )= Integral ( x, y in S ) x dx dy / Area ( P )
with the y coordinate of the centroid defined similarly.
One approach to computing the centroid of a Voronoi cell in 2D is simply to compute the areas and centroids of the component triangles (again, choosing an arbitrary base point to use in triangulation). We already know how to compute the area of a triangle. The centroid of a triangle is simply the average of the three vertices:
centroid ( T ) = ( (x1,y1) + (x2,y2) + (x3,y3) ) / 3
So the centroid of the polygon is found by adding up the centroids of the
component triangles, each weighted by its area, and dividing by the
sum of the areas of the triangles.
centroid ( P ) = sum ( T in P ) area ( T ) * centroid ( T )
/ sum ( T in P ) area ( T )
A second formula, for the X component of the centroid of the polygon, is
centroid_x ( P ) = 1/6 * sum ( 1 <= i <= N )
( x(i+1) + x(i) ) * ( x(i) * y(i+1) - x(i+1) * y(i) ) ) / Area ( P )
with a similar formula for the Y component.
Now suppose that instead of having the vertices of the Voronoi polygon around generator G, we have the list of neighbor generators. It is possible to compute the centroid of the Voronoi polygon directly from this information, using a formula given in Spatial Tesselations [Okabe].
The formulas for the centroid of a polygon given its vertices, or of a Voronoi cell given the sequence of Delaunay neighbors, are implemented in the GEOMETRY library.
Assuming we are only given the Delaunay information about a (finite) Voronoi cell, then we know we can draw a picture of the Voronoi polygon, because we just draw the perpendicular bisector line between the central node and all its Delaunay neighbors. So the information is there. But to analyze the polygon, we really want to know the coordinates of its vertices.
The key is the fact that each Delaunay triangle corresponds to a Voronoi vertex, and that the Voronoi vertex is the circumcenter of the Delaunay triangle. The circumcenter of a (nondegenerate) triangle is the center of the unique circle which passes through all three nodes.
The formula for coordinates (xc,yc) of the circumcenter depends on the fact that the vectors (x2-x1,y2-y1) and (x3-x1,y3-y1) are secants of the circle. Hence, each secant vector can be used to form a right triangle along with the diameter vector. Hence, in particular, the dot product of P12 = (x2-x1,y2-y1) with the diameter vector is equal to the squared length of P12, and similarly for P13. We end up having to solve the linear system:
(x2-x1) * xc + (y2-y1) * yc = (x2-x1)**2 + (y2-y1)**2
(x3-x1) * xc + (y3-y1) * yc = (x3-x1)**2 + (y3-y1)**2
to determine the circumcenter. Doing this for each Delaunay triangle
gives us the Voronoi vertices.
Suppose that we decompose each face F of the polyhedron P into triangles T. Then the volume of the polyhedron can be found by adding up the following terms:
Volume ( P ) = Sum ( F in P )
Sum ( T in F )
1/6 * ( x1 * y2 * z3 - x1 * y3 * z2
+ x2 * y3 * z1 - x2 * y1 * z3
+ x3 * y1 * z2 - x3 * y2 * z1 )
where the coordinates of the first vertex of triangle T are (x1,y1,z1),
and so on.
In order to compute the centroid of a polyhedron, we first pick a base point somewhere inside the polyhedron. Then we break each polygonal face into triangles. Then, on each triangle, we raise a tetrahedron to the base point. Now the polyhedron has been dissected into disjoint tetrahedrons.
It's easy to compute the volume of each tetrahedron. It's even easier to compute the centroid of each tetrahedron, since that's simply the average of its four vertices. But then it's simple to compute the centroid of the polyhedron, because that is simply the volume-weighted sum of the centroids of the constituent tetrahedrons:
centroid ( P ) = sum ( T in P ) volume ( T ) * centroid ( T )
/ sum ( T in P ) volume ( T )
In analogy to the 2D case, if we are given Delaunay information about a 3d "triangulation" of the region, we have a list of the Delaunay neighbor nodes. If we are careful, we can figure out all the sets of three neighbor nodes that, along with the center node, form a Delaunay tetrahedron.
As before, each Delaunay tetrahedron corresponds to a Voronoi vertex, and the Voronoi vertex is again the circumcenter of the Delaunay tetrahedron, which is now the center of the unique sphere which passes through all four nodes.
The formula for coordinates (xc,yc,zc) of the circumcenter depends on the fact that the vectors such as P12 = (x2-x1,y2-y1,z2-z1) are secants of the sphere. We end up having to solve the linear system:
(x2-x1) * xc + (y2-y1) * yc + ( z2-z1) * zc = (x2-x1)**2 + (y2-y1)**2 + (z2-z1)**2
(x3-x1) * xc + (y3-y1) * yc + ( z3-z1) * zc = (x3-x1)**2 + (y3-y1)**2 + (z3-z1)**2
(x4-x1) * xc + (y4-y1) * yc + ( z4-z1) * zc = (x4-x1)**2 + (y4-y1)**2 + (z4-z1)**2
to determine the circumcenter. Doing this for each Delaunay tetrahedron
gives us the vertices of the Voronoi polyhedron.
The formulas for the area and centroid of a polygon in 2D, the volume and centroid of a polyhedron in 3D, the circumcenter of a triangle in 2D or tetrahedron in 3D, or the area, centroid and vertices of a Voronoi polygon in 2D given the Delaunay neighbors, are all implemented in the routines:
Reference: