The Second Lunar Anomaly in Ancient Indian Astronomy
Dennis W. Duke, Florida State University
Links to a series of animations illustrating a variety of ancient lunar models are embedded in the following text:
All early Indian lunar models, from about A.D. 450 – 650, used only one anomaly – the variation in speed of the Moon as it circles the zodiac.[1] Unlike the Hipparchan model, which treated the same anomaly in terms of a single epicycle or its equivalent eccentric deferent, the Indian lunar (and solar) models without exception used the concentric equant, in which the Earth is at the center of a deferent with radius R = 1 and the center of uniform motion is some distance r from that center (see Figure 1). In such a model the equation of center q is given by
![]()
where the mean anomaly α = L – A, L is the Moon’s mean longitude, and A the longitude of its apsidal line.[2] For the concentric equant the apogee – the direction of slowest motion – is in the direction of the line from the earth to the equant point. The quality of the predictions of the concentric deferent and the Hipparchan model at syzygy are essentially equivalent.
The Laghumanasam, a short text by Munjala probably written around A.D. 930, gives much of the standard Indian planetary model information and appears to be derived from Aryabhata’s various texts, written ca. A.D. 500, Brahmagupta’s Brahmasphutasiddhanta, ca. A.D. 628, and the Suryasiddhanta, ca. sixth century A. D.[3] The Laghumanasam is a type of text known as a karana, which is a short work giving simplified and approximate rules for computing astronomical items. Among the rules that Munjala gives is a correction to the equation of center for the Moon in the form
![]()
where ![]() is the elongation of the
mean Sun from the lunar apsidal line, and
is the elongation of the
mean Sun from the lunar apsidal line, and ![]() is the
elongation of the mean Moon from the mean Sun. Yallaya, in a commentary to the Laghumanasam
written in A.D. 1428, claims that this correction was given earlier by
Vatesvara (ca. A.D. 904), but that earlier text has not been found and
the claim cannot be checked. What is most interesting is that this correction
is closely related to the second inequality of lunar motion known to Ptolemy,
and known today as evection. The first two terms in modern lunar theory are
conventionally written as
is the
elongation of the mean Moon from the mean Sun. Yallaya, in a commentary to the Laghumanasam
written in A.D. 1428, claims that this correction was given earlier by
Vatesvara (ca. A.D. 904), but that earlier text has not been found and
the claim cannot be checked. What is most interesting is that this correction
is closely related to the second inequality of lunar motion known to Ptolemy,
and known today as evection. The first two terms in modern lunar theory are
conventionally written as
![]() ,
,
with 2e = 6.29, ε = 1.27. The
first term is the elliptic inequality and the second is the evection. Noting
that ![]() and 2η – α = α – 2ψ, we have the
identity
and 2η – α = α – 2ψ, we have the
identity
![]()
and so the two modern terms can be rewritten as
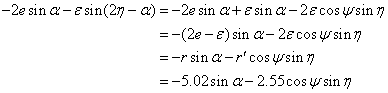
exactly the same form found in the Laghumanasam. Munjala’s numerical values imply a maximum value of about 2;29° for the second term in the final line, compared say to Ptolemy’s 2;40° and the modern 2;33°. The range of error for Munjala’s model is noticeably better than the error range for the full Almagest model (see Figures 2 and 3).[4]
Munjala’s expression is interesting on at least two other
counts. First, unlike the modern theoretical expression, in which the evection
term ![]() does not vanish at syzygy,
Munjala’s expression neatly isolates from the evection the part that
contributes only away from syzygy. Second, the empirical lunar anomaly that
remains after accounting for the principal term
does not vanish at syzygy,
Munjala’s expression neatly isolates from the evection the part that
contributes only away from syzygy. Second, the empirical lunar anomaly that
remains after accounting for the principal term ![]() can be written
as
can be written
as
![]()
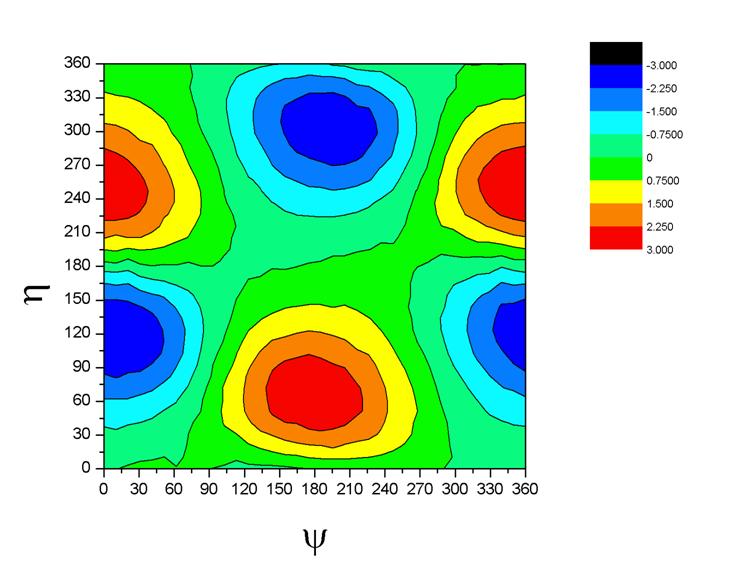
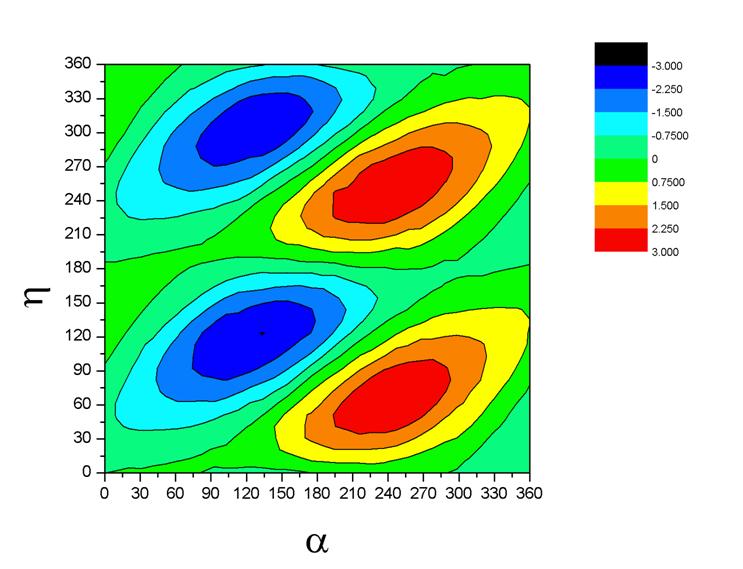
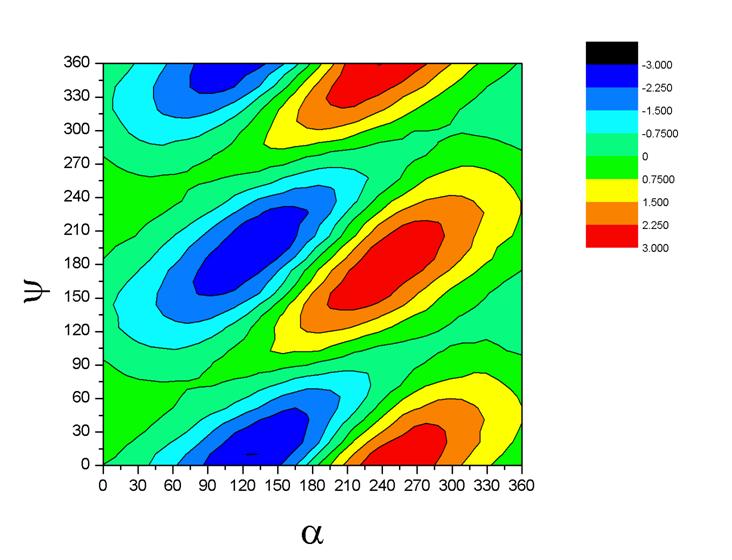
where λ is the lunar longitude, and this can be determined by a series of measurements of λ (or, in our case, calculations using modern theory), and is the empirical target that needs explanation by changing the simple lunar model to something more complicated. Of the three possible pair-wise combinations of the variables α, η, and ψ, Munjala’s term is expressed in terms of the pair (η,ψ) that happens to give the simplest empirical representation of the lunar anomaly after accounting for the first anomaly (see Figures 4-6). Whether the person responsible for the theory was aware of any of this, and the extent to which it played any role in the development of the theory, is, of course, impossible to determine based on the scant information we have.
Neither Munjala’s nor any other ancient Indian text gives a geometrical figure of any model, or discusses the derivation of any model. So while it could be the case that Munjala’s theoretical expression is derived from some Greek geometrical model of which we are already aware, such as the crank model given in the Almagest, it seems just as likely, if not more so, that Munjala’s expression is in fact an exact consequence of a simple underlying geometrical model, which may or may not have even been known to Munjala, recalling that under the Pingree – van der Waerden Hypothesis, the Indian texts summarize centuries old traditions inherited from the Greeks.[5] Without further information we cannot say whether the model was developed in India or in some earlier, and unknown to us, Greco-Roman tradition.
If the Laghumanasam expression was derived as an
exact consequence of some underlying geometrical model, then the model required
is straightforward to infer. We start with a concentric equant of eccentricity r
and imagine that the equant point oscillates on a small epicycle of radius ![]() centered
on the mean equant position (see Figure 7). The angle between the rotating
equant point and the mean lunar apsidal line is assumed to be 2ψ,
so the period of rotation is about seven months. The effect of this model is
that the equant eccentricity ρ oscillates between
centered
on the mean equant position (see Figure 7). The angle between the rotating
equant point and the mean lunar apsidal line is assumed to be 2ψ,
so the period of rotation is about seven months. The effect of this model is
that the equant eccentricity ρ oscillates between ![]() and
and
![]() ,
and the true lunar apsidal line oscillates about the mean apsidal direction by
an angle δ.[6] Thus at any instant the model
is a concentric equant with oscillating eccentricity and apsidal line,[7]
so
,
and the true lunar apsidal line oscillates about the mean apsidal direction by
an angle δ.[6] Thus at any instant the model
is a concentric equant with oscillating eccentricity and apsidal line,[7]
so
![]()
![]()
where
![]()
and δ is positive for ![]() and
negative for
and
negative for ![]() . Then
. Then
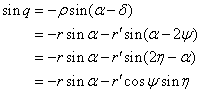
and so we have exact analytic correspondence between the geometrical model and Munjala’s expression.[8]
[For an animation of Fig. 7 see www.scs.fsu.edu/~dduke/munjala.html ]
An equivalent model can also be developed by letting the
small epicycle rotate through an angle 2η measured from the perigee
of the epicycle instead of 2ψ measured from the apogee (see Figure
8). In this case δ is positive for ![]() and negative
for
and negative
for ![]() , and we get
, and we get
![]()
and
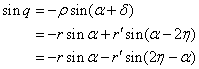
matching exactly the result from Figure 7. Therefore the models are equivalent, even though the small epicycle rotates in about seven months in Figure 7 and in about 15 days in Figure 8. Note that the exact equivalence of the two versions depends directly on the fact that for the concentric equant the Earth is always the same distance from the Moon. It is possible, of course, that some more complicated model could give the same expression, but it seems very unlikely that any simpler model could do so.
[For an animation of Fig. 8 see www.scs.fsu.edu/~dduke/shatir.html ]
The equivalence of the two models, in spite of the different rotation speeds, can also be understood from a simple geometrical analysis. First we need a preliminary result and a simple corollary (see Figure 9):
Theorem 1. Let EFG be an isosceles triangle, with EF = EG.
From the apex E drop a line to an arbitrary point P on the base FG, and extend
the line above E to point A. Let angle AEF = β, angle PEG = γ,
and angle EPF = α. Then ![]() .
.
Proof: since the triangle is isosceles, angle EFP = angle EGP. Then application of the fact that the sum of the internal angles of a triangle is 180° to triangles EFP and EGP establishes the result.
Corollary 1. Let angle β be measured
counterclockwise from EA, and let angle γ be measured
counterclockwise from EP. Let angles β and γ change
uniformly with time so that ![]() and
and ![]() . Then
angle EPF = α, measured counterclockwise from PE, also changes
uniformly with time, and with speed
. Then
angle EPF = α, measured counterclockwise from PE, also changes
uniformly with time, and with speed ![]() .
.
Now consider a large deferent with center at O and radius OM = R (see Figure 10). At a distance r from O place a smaller circle with
center E and radius EF = EG = ![]() . Let angle AEF = 2ψ
and angle PEG = 2η, and let ψ and η
increase uniformly with time at speeds ωψ and ωη.
Then triangle EFG is isosceles and we may apply Theorem 1 and Corollary 1. It
follows that
. Let angle AEF = 2ψ
and angle PEG = 2η, and let ψ and η
increase uniformly with time at speeds ωψ and ωη.
Then triangle EFG is isosceles and we may apply Theorem 1 and Corollary 1. It
follows that ![]() and the chord FG
subtended by angle FEG always makes an angle α with the apsidal
line AP, and that α increases uniformly with time with speed ωα
= ωψ + ωη. Also,
if we call OE the mean equant, in both length and direction, and OF and OG two
of the true equants, also in both length and direction, then the equation of
center q is the same for triangles MOF and MOG. Therefore the
geometrical analysis establishes exactly the same equivalence established above
using trigonometry. And since the construction is so simple, it seems extremely
likely that the equivalence could have been known in antiquity, even at a date
far earlier than Munjala’s A.D. 932.
and the chord FG
subtended by angle FEG always makes an angle α with the apsidal
line AP, and that α increases uniformly with time with speed ωα
= ωψ + ωη. Also,
if we call OE the mean equant, in both length and direction, and OF and OG two
of the true equants, also in both length and direction, then the equation of
center q is the same for triangles MOF and MOG. Therefore the
geometrical analysis establishes exactly the same equivalence established above
using trigonometry. And since the construction is so simple, it seems extremely
likely that the equivalence could have been known in antiquity, even at a date
far earlier than Munjala’s A.D. 932.
[For an animation of Fig. 10 see www.scs.fsu.edu/~dduke/munjala-shatir.html ]
The general model has (at least) two interesting special
cases. First, if we let β = γ = α and ![]() then
the two radii EF and EG will always point in opposite directions and FEG will
be a straight line which always makes an angle α with the apsidal
line AP. Thus this special case is exactly the concentric equant used for the
first anomaly alone, and we see that one way of understanding the full lunar
model is as a generalization of the concentric equant to allow
then
the two radii EF and EG will always point in opposite directions and FEG will
be a straight line which always makes an angle α with the apsidal
line AP. Thus this special case is exactly the concentric equant used for the
first anomaly alone, and we see that one way of understanding the full lunar
model is as a generalization of the concentric equant to allow ![]() while
keeping
while
keeping![]() . Whether this was part of the
path to discovery of the second lunar anomaly is, of course, impossible to say without
further information.
. Whether this was part of the
path to discovery of the second lunar anomaly is, of course, impossible to say without
further information.
[For an animation of this see www.scs.fsu.edu/~dduke/munjala-shatir-planets.html ]
A second special case has β = 0 and ![]() ,
and γ = 2α and
,
and γ = 2α and ![]() . Then the radius EF points
toward A and stays fixed, and the radius EG rotates counterclockwise with speed
2ωα. This model is then very closely related to the
planetary models of Ibn ash-Shatir (see the discussion below).
. Then the radius EF points
toward A and stays fixed, and the radius EG rotates counterclockwise with speed
2ωα. This model is then very closely related to the
planetary models of Ibn ash-Shatir (see the discussion below).
In the general case, with ![]() , the point where
chord FG crosses the apsidal line AP oscillates up and down, and so we
effectively have a pulsating eccentricity, and the pulsation is twice as
fast as the motion in anomaly, just as we see in many Indian texts. Thus it
could be that when the Indian texts speak of the varying lengths of the
eccentricities, they are not saying that we should vary them in the
calculation, but rather simply reminding us that their effective lengths are
changing. In reality, the Indian texts are so terse, and so generally devoid of
explanation of any kind, that this could easily be the case.
, the point where
chord FG crosses the apsidal line AP oscillates up and down, and so we
effectively have a pulsating eccentricity, and the pulsation is twice as
fast as the motion in anomaly, just as we see in many Indian texts. Thus it
could be that when the Indian texts speak of the varying lengths of the
eccentricities, they are not saying that we should vary them in the
calculation, but rather simply reminding us that their effective lengths are
changing. In reality, the Indian texts are so terse, and so generally devoid of
explanation of any kind, that this could easily be the case.
Also, one way of looking at these models is in terms of eccentricities and epicycle radii that are oscillating in both length and direction. This is then very similar to the various intermediate steps of the algorithms of the Indian models. Thus there could be some relation between the Indian models and the double epicycle approximation to the equant – that is, it seems possible that the Indian algorithms are approximations to the equant via some combination of double epicycle implementations of both planetary anomalies.
Both versions of the model can be changed from concentric deferent to eccentric deferent, and then the equations of center would be given by
![]() or
or ![]()
In eccentric deferent models the Earth-Moon distance is the
denominator in these expressions and so is, of course, not a constant. Hence
the equations of center ![]() and
and ![]() are
not strictly equal, but the differences are small since, as shown above, the
numerators are the same, and the differences in the denominators are
proportional to the small quantity
are
not strictly equal, but the differences are small since, as shown above, the
numerators are the same, and the differences in the denominators are
proportional to the small quantity ![]() . The equivalent
double-epicycle version of the eccentric deferent is, of course, the basis of
Ibn ash-Shatir’s lunar model,[9] so it is a variant of the Munjala
model with (a) exchanging the concentric equant with an eccentre or equivalent
large epicycle, (b) counting the angles as in Figure 8, and (c) putting the
small epicycle in various places in the figure. One such variant – putting the
small epicycle on the tip of the large epicycle – was adopted by Copernicus.[10] The earliest known Arabic lunar (or
planetary) models date to about A.D. 1240, however, so we are not in position
to say whether Munjala’s model was somehow transmitted to the Arabic
astronomers or whether they developed it independently.
. The equivalent
double-epicycle version of the eccentric deferent is, of course, the basis of
Ibn ash-Shatir’s lunar model,[9] so it is a variant of the Munjala
model with (a) exchanging the concentric equant with an eccentre or equivalent
large epicycle, (b) counting the angles as in Figure 8, and (c) putting the
small epicycle in various places in the figure. One such variant – putting the
small epicycle on the tip of the large epicycle – was adopted by Copernicus.[10] The earliest known Arabic lunar (or
planetary) models date to about A.D. 1240, however, so we are not in position
to say whether Munjala’s model was somehow transmitted to the Arabic
astronomers or whether they developed it independently.
[For animations of all the lunar models see www.scs.fsu.edu/~dduke/copernic2.html ]
[For an animation of Ptolemy’s lunar model see www.scs.fsu.edu/~dduke/moon6.html ]
[For animations of the equivalent eccentric version of Ptolemy’s lunar model see www.scs.fsu.edu/~dduke/moon10a.html ]
If we put the center E of the small epicycle at some point north of the center of the deferent, and the Earth at some point south of the center, then the various Arabic planetary models are very closely related to the second special case mentioned above. It is well known, of course, that such models are very close approximations to the Ptolemaic equant.[11]
[For animations of all the Arabic planetary models see www.scs.fsu.edu/~dduke/arabmars.html ]
[For an animation of the equivalent eccentric version see www.scs.fsu.edu/~dduke/shatir-planets.html ]
Although Ptolemy does not discuss the Almagest lunar model in terms of an oscillating eccentricity and apsidal line, the final analytic expression for his crank mechanism plus epicycle model with a shifted apsidal line can be written in the form[12] (see Figure 11)
![]() ,
,
and from the discussion above we know that such a model can always be transformed into an equivalent eccentric model, and in this case the apsidal direction, but not the eccentricity, oscillates around a mean value. The relation of the Almagest model to the Munjala model, if any, is obscure.
[For an animation of Ptolemy’s lunar model see www.scs.fsu.edu/~dduke/moon6.html ]
[For animations of the equivalent eccentric version of Ptolemy’s lunar model see www.scs.fsu.edu/~dduke/moon10a.html ]
The eccentric version of the Laghumanasam model has an interesting subsequent history.[13] Essentially the same model, with the small epicycle rotating through the angle 2ψ, was used by Kepler at an intermediate stage of his lunar research, and then abandoned. The model was later used by Philip Lansbergen with the small epicycle rotating through the angle 2η, and so was essentially the lunar model of ash-Shatir (and hence Copernicus) transformed so that the small epicycle was at the center of the eccentric deferent. Jeremiah Horrocks, post-Kepler but pre-Newton, again used the model in the form of Kepler, with the small epicycle rotating through the angle 2ψ, the only significant difference being that for Horrocks the deferent was a Keplerian ellipse.
So we see that the physical idea of an oscillating lunar eccentricity and apsidal line was certainly known as early as medieval India and perhaps back to Greco-Roman times. It was used and perhaps re-discovered by Arabic astronomers, by Copernicus, and by various post-Copernican astronomers, including Kepler, van Lansbergen, and Horrocks. And finally, it was the crucial clue Newton borrowed from Horrocks to finally formulate his own lunar model.[14]
|
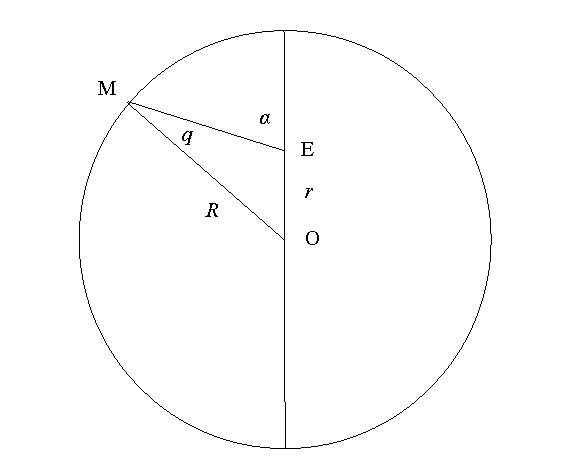
Figure 1. In the concentric equant model the Earth is at the
center O of a deferent of radius R and the moon is at M on the deferent.
The motion of M is uniform as seen from the equant point E, which is a distance
r from O, so angle AEM = α increases uniformly with time.
Angle OME = q is the equation of center, and is given by ![]() .
.
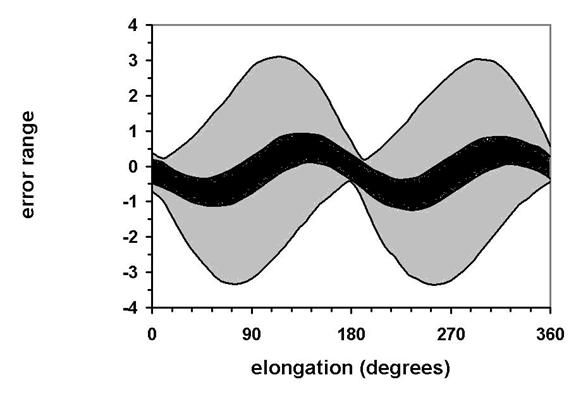 Figure 2. The
Indian lunar model error range for the simple model with one anomaly (outer
grey area) and the Munjala model (inner black area).
Figure 2. The
Indian lunar model error range for the simple model with one anomaly (outer
grey area) and the Munjala model (inner black area).
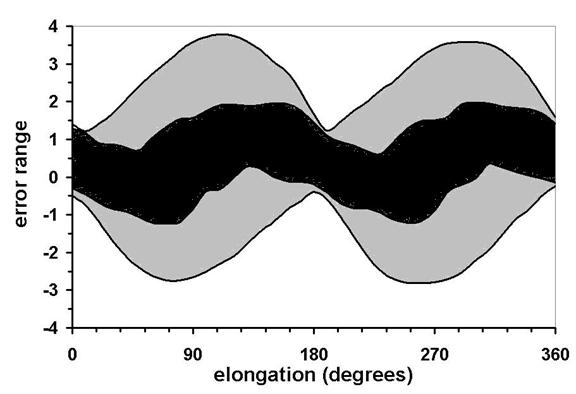 Figure 3. The Almagest
lunar model error range for the simple model with one anomaly (outer grey area)
and the full model with the crank mechanism and the shifted apogee (inner black
area).
Figure 3. The Almagest
lunar model error range for the simple model with one anomaly (outer grey area)
and the full model with the crank mechanism and the shifted apogee (inner black
area).
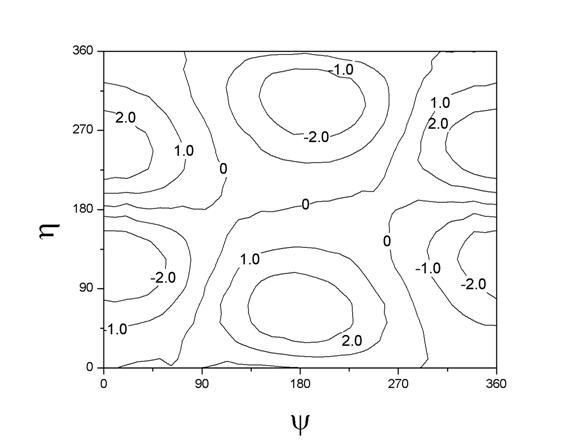 Figure 4.
Figure 4.
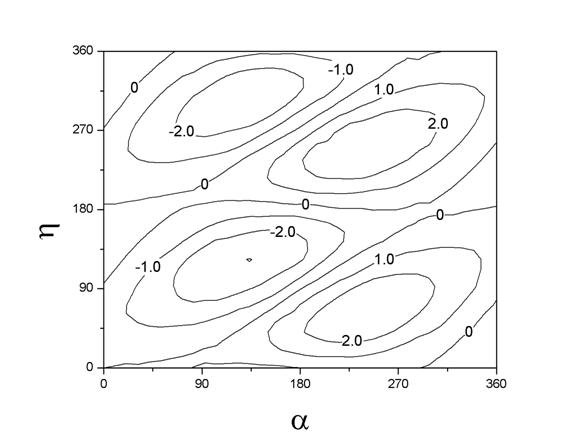 Figure 5.
Figure 5.
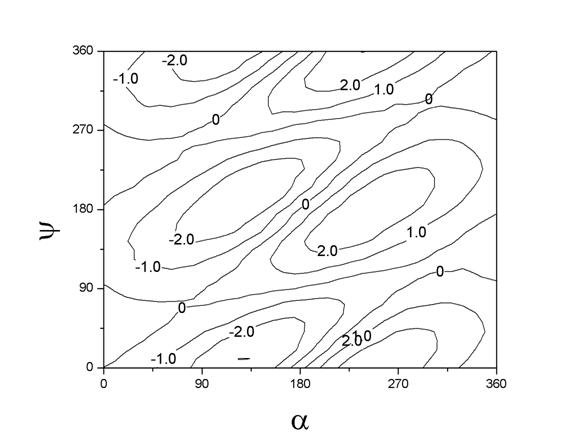 Figure 6.
Figure 6.

Figure 7. Moon at M, Earth at center O, mean equant at E, OE = 2e, true equant at E´, OE´ = ρ. Radius of small epicycle is ε and rotates counterclockwise.
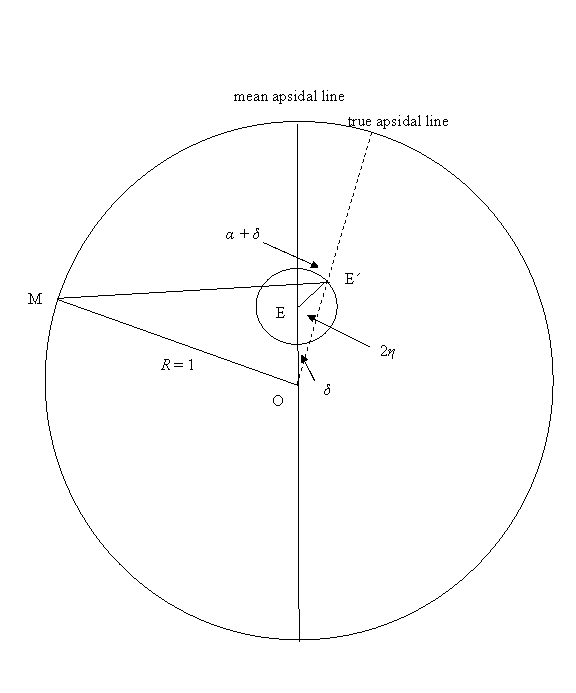
Figure 8. Moon at M, Earth at center O, mean equant at E, OE = 2e, true equant at E´, OE´ = ρ. Radius of small epicycle is ε and rotates counterclockwise.
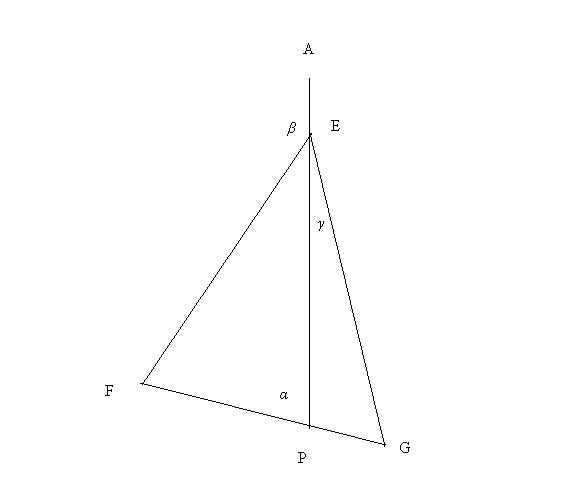
Figure 9.
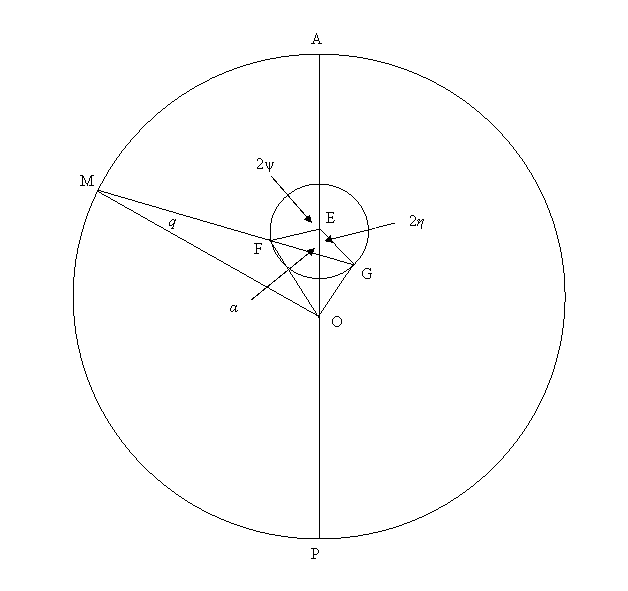
Figure 10.
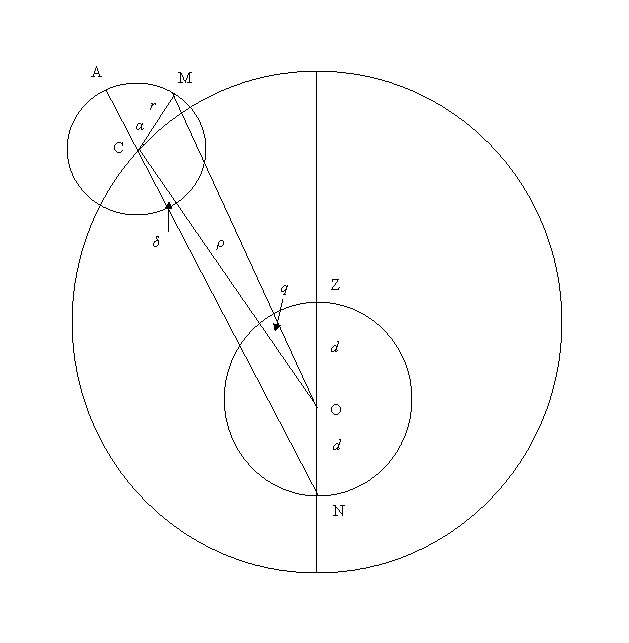
Figure 11. The Almagest lunar model. The Moon is at M on an epicycle centered at C with radius CM = r. Z is the center of a deferent of radius ZC = R. Angle ZOC = 2η is twice the lunar elongation, so the motion of C is uniform with respect to the Earth at O, and the model is a form of concentric equant with the Earth at the position of the equant rather than the center of the deferent. The distance OC = ρ is variable, and OC = ON = d. The apogee of the epicycle is the extension of NC to A, and angle CAN = α is the mean anomaly, which increases uniformly. Angle NOC = δ is used to in the computation of the equation of center q.
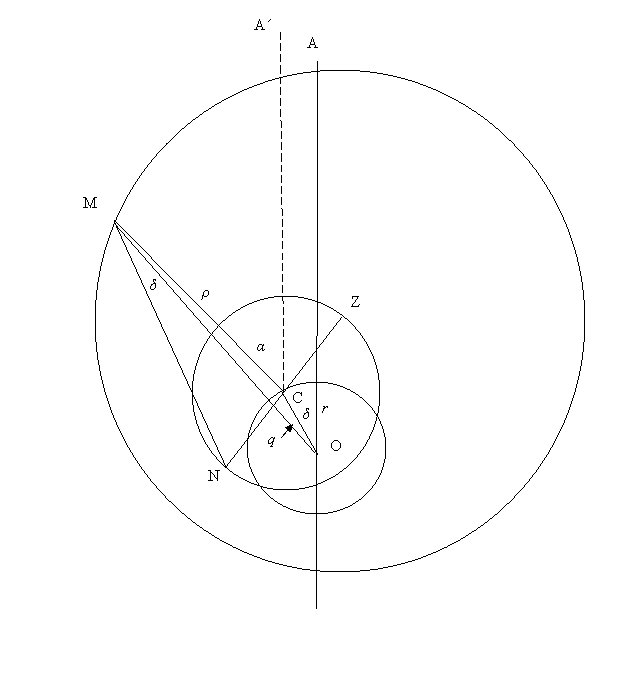
Figure 12. The equivalent eccentric form of the Almagest lunar model. The Moon is at M on a deferent centered at Z with radius ZM = R. Z is on a circle with center C and radius d, and Z rotates such that angle ZCM = 2η. C oscillates about the direction OA such that angle AOC = angle OMN = δ. The distance CM = ρ is variable. The apogee of the mean eccentricity is A, and the extension of the line OC is the direction of the true eccentricity Angle A´CM = α is the mean anomaly, which increases uniformly with time.
color version of Figure 4
color version of Figure 5
color version of Figure 6
[1] D. Pingree, “History of Mathematical astronomy in India”, Dictionary of Scientific Biography, 15 (1978), 533-633.
[2] D. Pingree, “Concentric with Equant”, Archives Internationales d’Histoire des Sciences, 24 (1974) 26-28.
[3] K. S. Shukla, A Critical Study of the Laghumanasa of Manjula, New Dehli (1990); D. Pingree, ibid. (ref. 1) 618-619.
[4] These figures are modeled after those in V. Petersen, “The Three Lunar Models of Ptolemy”, Centaurus, 12 (1969) 142-171. This paper explains all the details of the full lunar model found in the Almagest.
[5] D. Pingree, ibid. (ref. 1-3), and references therein; B. L. van der Waerden, “The heliocentric system in greek, persian, and indian astronomy”, in From deferent to equant: a volume of studies in the history of science in the ancient and medieval near east in honor of E. S. Kennedy, Annals of the new york academy of sciences, 500 (1987), 525-546, and references therein.
[6] Such models with oscillating eccentricity permeate Indian texts, of course, and this is the first case I know of that we might finally understand the background of such things.
[7] S. B. Gaythorpe, “On Horrocks’s Treatment of the Evection and the Equation of Center, with a Note on the Elliptic Hypotheses of Albert Curtz and its Correction by Boulliau and Newton”, Monthly Notices of the Royal Astronomical Society, 85 (1925) 858-65.
[8] It might be that this model is foreshadowed in Brahmagupta’s Brahmashputasiddhanta (ca. A.D. 628), which also has similar oscillations of the orbit elements for the Sun and Moon. See D. Pingree ibid. (ref. 1) p 569, top right, and p 569, center left, but either the text or the translation is too jumbled to be sure what it means.
[9] V. Roberts, “The Solar and Lunar Theory of Ibn ash-Shatir”, Isis, 48 (1957) 428-432.
[10] O. Neugebauer, “On the Planetary Theory of Copernicus”, Vistas in Astronomy, 10 (1968) 89-103.
[11] E. S. Kennedy, “Late Medieval Planetary Theory”, Isis, 57 (1966) 365-378; G. Saliba, A History of Arabic Astronomy, (New York, 1994).
[12] V. Petersen, ibid. (ref. 4) p 160.
[13] C. Wilson, “On the Origin of Horrocks’s Lunar Theory”, Journal for the history of astronomy, 18 (1987), 77-94; C. Wilson, “Predictive Astronomy in the century after Kepler”, in Taton and Wilson, General History of Astronomy, 2A (1989) 161-206.
[14] C. Wilson, “Newton on the Moon’s Variation and Apsidal Motion”, in Buchwald and Cohen, Isaac Newton’s Natural Philosophy, (Cambridge, 2001).