Newton’s approach to Kepler’s area law

First, consider an observer at point S and a body moving under its own inertia along the line ABC…. For equal time intervals, the segments AB, BC, etc are equal in length. Furthermore, the areas of the successive triangles SAB, SBC, etc are also equal, since the base of each triangle is the same and the heights are also the same (the distance of S from the line ABC).

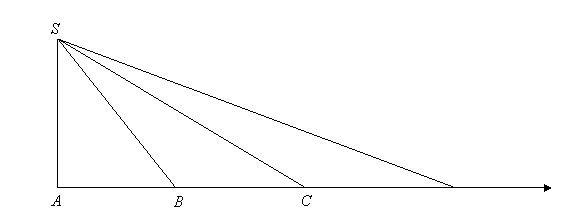Figure 1

Now suppose that when the body reaches point B it receives an (instantaneous) impulse directed along the line from B to S (i.e. an impulse resulting from some sort of central force). The velocity of the body, but not its position, will change, and the body will take a new path to point C, as shown below:

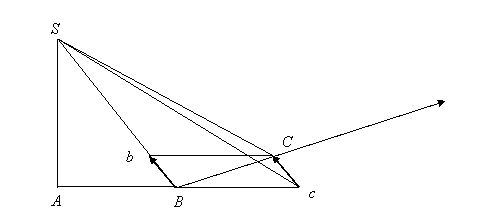Figure 2

In this figure, point c now marks the place where the body would have gone in absence of the impulse (as in the first figure), point b is where it would go due solely to the impulse, and point C is where it actually does go under the combined influence of both effects. However, since BbCc is a parallelogram (due to the vector-sum nature of the velocities), triangles SBC and SBc have the same (common) base and the same height (since points C and c are equidistant from the line SB), and hence the same area, which is also the same area as triangle SAB, as shown above. The procedure can be repeated indefinitely, and all succeeding triangles will have the same area as the initial triangle SAB. Furthermore, in the limit that the time interval between impulses becomes infinitesimal, the path of the body will become a continuous curve.

In this way Newton proves that in the presence of a central force, or no force, a moving body sweeps out equal areas in equal times. And as the story goes, Newton was so unimpressed with Kepler’s understanding of the area law, and/or so impressed with his own, that he did not even mention Kepler by name in Book 1 of the Principia.

The accompanying animation will show Figure 1 if you slide the impulse to zero, and Figure 2 for a finite impulse.