A Brief Introduction to Ancient Planetary Models
The animations illustrate the models of planetary motion found in the Almagest, by Claudius Ptolemy, and some of the models formulated by Arabic astronomers that correct some of the (as felt at the time) theoretical shortcomings of the Almagest models.
The Issues: the first and second anomalies
The ancient astronomers thought of the Sun, the Moon, and the five planets easily visible to the naked eye (Mercury, Venus, Mars, Jupiter, and Saturn) as wandering stars. Thus while the ordinary stars maintained fixed positions in the sky relative to each other, the seven planets were observed to move relative to each other and to the fixed stars. The principal motion of the planets was a regular west-to-east motion generally along the ecliptic, and the ancients had good values for the average (mean) speed of each planet. In addition, however, the planets were observed to have two anomalies to their otherwise regular motion:
(1) the speed of each planet around the ecliptic was not constant. Instead there was a point of minimum speed (the apogee) and a point of maximum speed (the perigee). A point of substantial interest to the astronomers was how the speed of each planet varied as it moved around the ecliptic. This irregularity was called the first anomaly, or the zodiacal anomaly.
(2) The orbit of each planet had a special relationship to the position of the Sun, and was called the second anomaly, or solar anomaly. For Mars, Jupiter and Saturn, the orbit of the planet is observed to stop its forward (west-to-east) motion, reverse direction, stop again, and finally resume forward motion. This retrograde motion happens when the planet is about 180° away from the Sun. On the other hand, both Venus and Mercury are never observed too far from the Sun, but also show the same pattern of retrograde motion. For those two planets, however, retrograde takes the planet to the same longitude as the Sun, and hence it is visibly lost in the glare of the Sun. Thus the observable quantity of interest for those planets was the greatest elongation, or angular distance from the (mean) Sun.
The Sun’s motion exhibits only the zodiacal anomaly, and while the Moon does not exhibit retrograde motion, its motion is nevertheless the most complex and variable of all the planets. Thus the great triumph of the ancient models was to quantitatively account for not only the general regular motion of each planet, but also both the zodiacal and solar anomalies, and most importantly, how those two anomalies interact with each other.
Uniform Circular Motion
The theoretical framework of all the ancient models was a principle going back at least to Aristotle: a belief that the ‘natural’ motion of a celestial body was around a circle, and the motion must be uniform when viewed from the center of that same circle. In order to approximate reality, it was allowed to have circles rotating about other circles, or epicycles, and/or to have circles not centered on the Earth (the assumed center of the universe). It is an interesting historical fact that of the planetary models in the Almagest only the model for the Sun respects these principles. All the others use one or more mechanisms that break the rules, but invariably produce results for the orbits in better agreement with observation. One of the triumphs of Arabic astronomy was to produce planetary models which agree with observation as least as well as the Almagest models, but also (almost) completely respect the principle of uniform circular motion.
The Sun and the simple Moon
Here is how the orbits work, progressing from the simplest to the more complicated. The simplest case is to have the Earth at the center of a deferent circle with the planet moving with uniform speed around the deferent, always counterclockwise. In such a model the motion of the planet as seen from the Earth will be completely uniform with no anomalies, and such simple motion is not seen for any of the planets. The simplest complication is to use one of two equivalent mechanisms to account for a motion with a zodiacal anomaly. One can either make the deferent circle somewhat eccentric with respect to the Earth, or one can leave the Earth at the center of the deferent and instead put the planet on a small epicycle circle which is itself centered, and moving upon, the circumference of the deferent. Always assuming counterclockwise motion on the deferent, if the motion of the planet on the epicycle is clockwise (within certain limits), then the planet will always move forward (counterclockwise) and will exhibit a simple zodiacal (or first) anomaly. The animations show two such cases. For the Sun, the motion along the deferent is at the same speed and opposite in direction to the motion on the epicycle (measured relative to a rotating radius of the deferent), while for the simplest lunar model the motions are (slightly) different. Such models are illustrated in the animations of the Sun and the simple Moon, a model which is accurate only at syzygy, i.e. when the Sun-Moon elongation is either 0° or 180°. Using the slider control one can move between the epicycle and eccentric models and verify that the planet follows exactly the same path in both models.
The Planets
The next most complicated model would combine an epicycle and an eccentric deferent. If the motion of the planet on the epicycle is now counterclockwise, then (within certain parameter limits) the planet will exhibit retrograde motion as required by the second anomaly, and by virtue of the eccentric deferent will also have the zodiacal anomaly. Although it is virtually certain that such models were explored as options for describing the motion of the planets, it turns out that such models fail to account properly for the interaction between the first and second anomalies (although, for Jupiter and Saturn, the discrepancies are hard to establish with naked-eye observations). The solution to this problem that is given in the Almagest models is to introduce yet another complication, this one violating the principle of uniform motion. Thus, while keeping the center of the planet’s epicycle moving upon a circular deferent, eccentric with respect to the Earth, one assumes that the mean motion of the planet, i.e. the motion of the center of the epicycle, is uniform not with respect to the center of the deferent, but with respect to a point – the equant – displaced from the center of the deferent. In the case of Venus, Mars, Jupiter and Saturn, the center of the deferent bisects the distance between the Earth and the equant. In the case of Mercury, the position of the equant bisects the line between the Earth and the center of the deferent (and Mercury has yet another complication). The result in all cases is fairly good quantitative agreement between the model predictions for the variation in the width of the retrograde arcs (or the size of greatest elongation) with position of the planet on the ecliptic.
Complications for Mercury and the Moon
For Mercury, the Almagest model uses an additional complication (or feature), as mentioned above. The center of the deferent circle is itself placed on the circumference of a small circle which rotates clockwise. For the Moon, the final model uses a similar mechanism to create a moving deferent, and in addition the position of the Moon in its epicycle is measured from a line extending from the opposite side of the small crank circle to the center of the epicycle. The result is that the models for Mercury, and especially the Moon, have fairly good agreement with observation of the angular position of the bodies, but rather poor agreement with the distance of each body from the Earth. This latter issue was not observable to the ancient astronomers for Mercury, but it is a factor 2X effect for the Moon, and was one of the problems that most concerned the Arabic astronomers (and later, Copernicus).
The Arabic Planetary Models
The various Arabic models for the planetary motions have two general qualities: they agree quite well with the angular motions as given by the Almagest models, and they also (almost) completely respect the principle of uniform circular motion. In these models the equant is abandoned in favor of a pair of epicycles (or their geometric equivalent). In addition, the Arabic models for Mercury and especially the Moon show marked improvement with observation for the variation in Earth-planet distance. Essentially exact copies of the Arabic models were used by Copernicus, but it is still not known how he learned about the models.
The Transformation from a Geocentric to a Heliocentric Point of view
Finally, while all the discussion to this point has been in terms of geocentric models, it is very easy to see the relation of these models with heliocentric models, at least in a qualitative way. There are two cases:
I. Geocentric to Heliocentric for a Superior Planet

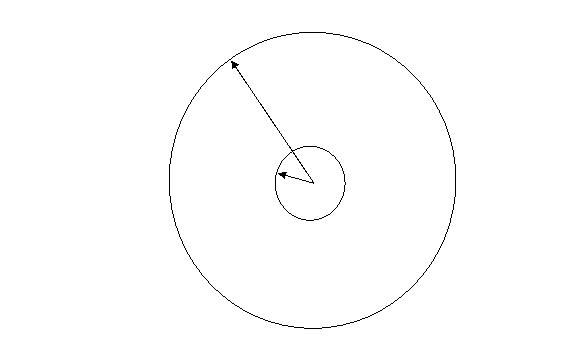
Starting position: The Earth is at the center of a large circle which carries the epicycle. The planet is on the epicycle, and the radius vector of the planet on the epicycle is parallel to the vector (dotted) from the Earth to the (mean) Sun.
We now swap the epicycle for a moving eccentre. In modern terms, we just add the long vector and short vector in reverse order to the above:
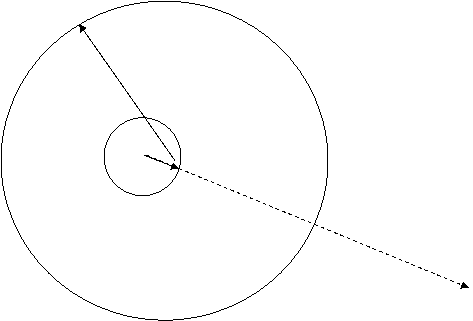 |
The model is still geocentric, the large circle is now centered on the tip of the short vector, and the short vector still points in a direction parallel to the mean Sun. This model is exactly what we have in Almagest XII. Finally, you can make this Tychonic by shortening the dotted vector so that it coincides with the short vector, thus putting the Sun at the tip of the short vector.
To go heliocentric, we need a lemma:
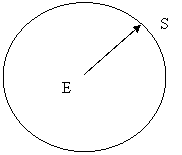 |
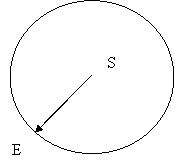 |
||
and
are both logically equivalent representations of the same physical system, one as seen from the Earth, the other as seen from the Sun. From either reference frame, whatever is orbiting the Sun when it is moving (e.g. a planet) is also orbiting it when it is at rest, and similarly for the Earth (which has the Moon, not shown, orbiting it). So if we move the Sun into the eccentre in the second figure above, and invoke the lemma, we get
which is pure Copernican heliocentrism.
II. Geocentric to Heliocentric for an Inferior Planet
Now for an inner planet (say Venus), we start again with the classical geocentric view, with the mean Sun (dotted vector) always pointing to the center of the epicycle:
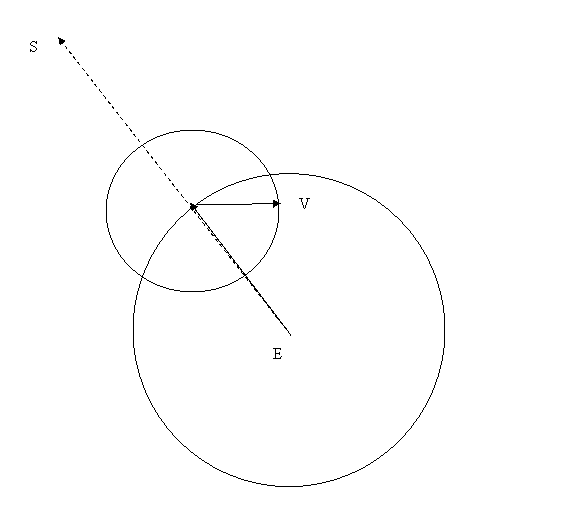
The simplest thing to do is
- move the mean Sun to the center of the epicycle, which gives the Tychonic model, and
- immediately invoke the lemma, swapping Earth and Sun, which gives the heliocentric model:

REFERENCES
All of the above is explained in much greater detail in many places. Two good places to look first are:
James Evans, The History and Practice of Ancient Astronomy, Oxford University Press (1998)
Hugh Thurston, Early Astronomy, Springer (1994).